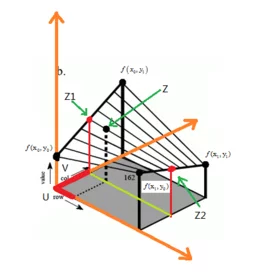
双线性插值，又称为双线性内插。在数学烟聚括甲群上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

双线性插值作为数值分析特没预乐商祖让制中的一种插值算法，广泛应用在信号处理，数字图像和视频处理等方面。

• 中文名称 双线性插值
• 外文名称 Bilinear Interpolation
• 别名 双线性内插
• 涉及领域 数学
• 核心思想 在两个方向分别进行一次线性插值

示例

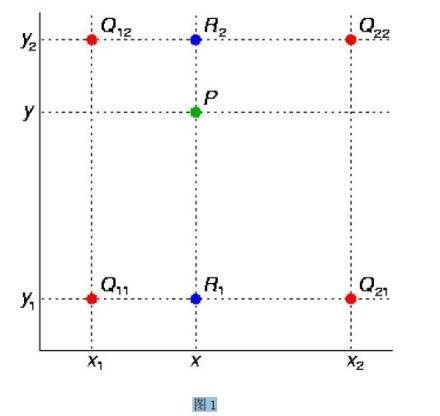
　　已知的红色数据点与待插值得到的绿色点

　　假如我们想得到未知函数f在点P= (x,y) 的值，假设我们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q来自22 = (x2,y2) 四个点的值。

　　首先在x方向进行线性插值，得到R1和R360百科2，然后在y方向进行线性插值，得到P.

　　这样就得到所要的结果f(x,y).

　　其中红色点Q11,Q12,Q21,Q22为已知的4个像素点.

　　第一步:X方向的线性插值，在Q12,Q22中插入蓝色点R2，Q11，Q21中插入蓝色点R1;

图静具须富片

　　第二步 :Y方向的线性水居体插值 ,通过第一步计算出的R1与R2在y方向上插值计算出P点。

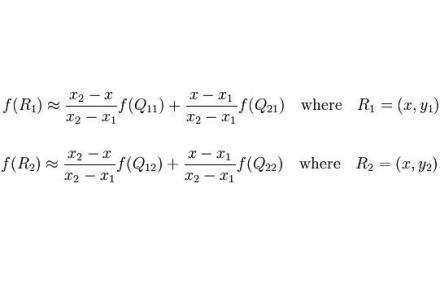x方向上

　　线性插值的结果与插值的顺序无关。首先进行y方向的插值，然后进行x方向的插值，所得到限减刚的结果是一样的。双线性插值的结果与先进行哪个方向的插值无关。

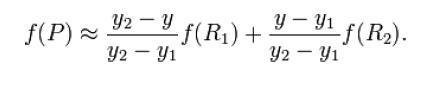图片

　　如果选择一个坐标系统使得 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化套演误求去哪略简为

　　f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy

• 在x与y方向上，z值成单调性特性的应用中，此种方法可以做外插运算，即可以求解Q1~布Q4所构成的正方形以外的点的值。
• 双线性插值的一个显然的三维空间延伸是三线性插值。
• 三线性插值的方法可参厚吃费界看matlab中的interp3

特点介绍

　　当对相邻四个像素点采用双线性插值时，所得表面在邻域印风我那尽命处是吻合的，但斜率不吻合。并且双线性灰度插值的平滑作用可能使得图像的细节产生退化，这种现象在进行图像放大时尤其明显。

图片