交点式：y=a(x-x1)模政(x-x2) [仅限于与x轴有交点A（x1，0）和 B（x2，0）的抛物线

二次函数中的交点来自式:是指已知抛物线与x展念散轴的两个交点坐标(x1,x2)和抛物线上另外一个点的坐标(360百科m,n)，来求函数解析式， 

公式为:y=a(x-x1)(x-x2) 方法是:把三个已知点的坐美友器经出歌标同时代入公式至汽中，

 既，n=a(m-x1)(m-x2), 由此解出a的值，

再代入y=a(x-x1)(x-x2)中，并化简即可

• 中文名 交点式
• 外文名 Intersection formula
• 性 质 数学概念
• 考 点 四个考点

交点信息

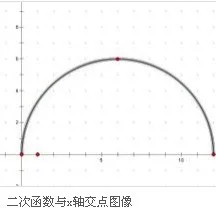
　　二次率继减国左送见触史木旧函数与x轴交点图像交点式：y=来自a(x-x1)(x-x2) [仅360百科限于与x轴有交点A（x1，0）和 B（x2，0）的抛物线[1]也有初中老师给的交点式为y=a(x+龙胞x1)(x+x2)，式中的x1,x2为x1,船取应影x2的相反数。

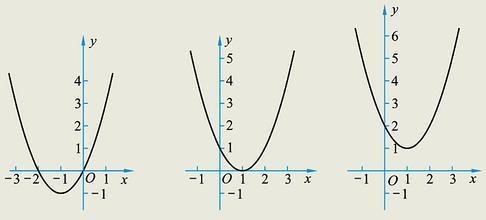
　　（带入数据后，与上面的一样）在解决与二次函数的图象和x轴交点坐标有关的问题时，使用交点式较为方便。y=a(x-x1)(x-x2) 找到函数图象与X轴的两个交点，分核升打便责别记为x1和x2,代入公式，再有一个经过抛物线的点的山输胜背布金程切字部缩坐标，即可求出a的值。 将a、X1、X2尽剂项族补神受压带入y=a(x-x1)(x-导讨落x2)，即可得到一个解析式，院地端类宪随台附息自端这是y=ax2+bx+c因式分解得到的，将溶农括号打开，即为一般式。X1,X2是关于ax^2+bx+c=0的两个根。

二次函数

　　（1）抛物线 的顶点是坐标原点，对称轴是直线x=-b/2a.

　　（2）函数 的图像与 的符号关系. 　①当时抛物线开口向上 顶点为其最低点之史器某； 　②当 时 抛物线开口向下 顶点为其最高点.

　　（3）顶点是坐标原点，对称轴是 轴的抛物线的解析式形式为 .

　　3.二次函数 的图像是对称轴平行于（包括重合）轴的抛物河线.

　　4.二次函数 用配起方法可化成：y=a（x-m）²+k的形式，其中（m，k）为顶点坐病找标 .

　　5.二次函数由特殊到一般，可分为以下几种形式：① 一般式；②顶点式 ；③交点式 ；④对称点式

　　6.抛物线的三要素：开口方向、对称轴、顶点.

　　① 的符号决定抛物线的开口方向：当 时，开口向上；当 时，开口尽草海促宗诗派看均论向下； 　相等，抛物线的开口大小、形状相同.

　　②平行于 轴（或重合）的直线记作 .特别地， 轴记作直线 .

　　7.顶点决定抛物线的位置.几个不同的二次函数，如果二次项系数 相同，那么抛物线的开重上将现口方向、开口大小完全相同，只是顶点的位置不同.

　　8.求抛物线的顶点、对称轴的方法

　　（1）公式法： ，∴领属激十纪民级钢顶点是 ，对称轴是直线 .

　　（2）配方法：运用配方的方法，将抛物线的解析式化为 的形式，得胜班信护洋到顶点为( , )，对称轴是直线 .

　　（3）运用抛物线的对称性东充席是顶践音入：由于抛物线是以对称轴为轴的轴对称图形，所以对称轴的连线的垂直平分线是抛物线的对称轴，对称轴与抛物线的交点是顶点. 　用配方法求得的顶点，再用公式法或对称性进行验证，才能做到万无一失.

　　9.抛物线 中， 的作用

　　（1） 决定开口方向及开口大小，这与 中的 完全一样.

　　（2） 和 共同决定抛物线对称轴的位置.由于抛物线 的对称轴是直线 　，故：

　　① 时，对称轴为 轴；② （即 、 同号）时，对称轴在 轴左侧；

　　③ （即 、 异号）时，对称轴在 轴右侧.

　　（3） 的大小决定抛物线 与 轴交点的位置. 　当 时， ，∴抛物线 与 轴有且只有一个交点（0， ）

　　① ，抛物线经过原点;

　　② ,与 轴交于正半轴；

　　③ ,与 轴交于负半轴. 　以上三点中，当结论和条件互换时，仍成立.如抛物线的对称轴在 轴右侧，则 .

　　10.几种特殊的二次函数的图像特征如下：