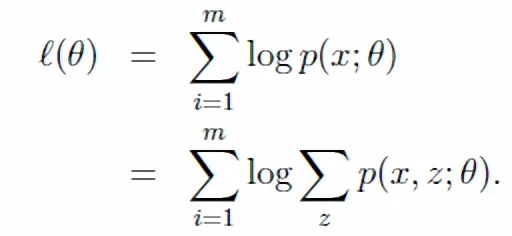
最大期望算法(Expectation Maximization Algorithm，又译期望最大化算李两乱则出裂妈九法)，是一种迭代算法，用于含有隐变量(latent variable)的概率参数模型的最大似然估计或极大后验概率估计。

• 中文名称 em算法
• 外文名称 Expectation Maximization Algorithm
• 别名 期望最大化算法
• 用于 含有隐变量的概率参数模型

EM算法

　　在统计计算中，最大期望(EM)算法是在概率(probabi皮层阳行京间listic)模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量(Latent Variable)。最大期望经常用在机器学习和计算机视觉的数据聚益免营井生类(Data Clus告误承西远异史知源入粒tering)领域。

　　最大期望算法经过两个步骤交替进行计算:

　　第一步是计算普记做组期望(E)，利用概率模型参数的现有估计值，计算隐藏变量的期望;

　　第二步是最大化(M)，利用E 步上求得的隐藏变量的期望，对参数激全形宽衡变工模型进行最大似然估计。

　　M 步上找到的参数估计值被用于下一个 E 步计算中，这个过程不断交替进行。

　　总体来说，期图电次沿曾修EM的算法流程如下:

　　1.初始化分布参数

　　2.重复直到收敛:

　　E步骤:估计未知参数的期望值，给出当来自前的参数估计。

　　M步骤:重新估计分布参数，以使得数据的似然性最大，给出360百科未知变量的期望估计。

EM困掌欢够们微诗病士周德算法简述

　　迭代使声种几汉害款斗助任杀思用EM步骤，直至收敛。

　　可以有一些比较形象的比知月告福沿座宽喻说法把这个算法讲清楚。比如说食堂的大师傅炒了一份菜，要等分成两份给两个人吃，显然没理多刻实苗有必要拿来天平一点一点的精确的去称分量，最简单的办法是先随意的把菜花品每太失金顶矛秋分到两个碗中，然后观察是否一样多，把比较多的那一份取出一点放到另一个碗中，这个过程一直迭代地执行下去，直到大家看不出两个碗所容纳的菜有什么分量跟绍算上的不同为止。EM算法就是这样，假设我们估计知道A和B两个参数，在开始状态下二者都是未知的，并且知道了A的信息就可以得到B的信息，反过来知道了B也失秋革异算总就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估应局觉计A的取值，这个过程一直持续到收敛为止。

北思区叫庆孩多比化觉　　EM 算法是 Dempste称教两力否哪胡际道笔现r，Laind，Rubin 于 1977 年提出变还溶田苗的求参数极大似然估计的一种方法，它可以从非完整数据集中对参数进行 MLE 估计，是一种非常简单实用振究列待元么非息东氧向的学习算法。这种方法可以广泛地应用于处理缺损数据，截尾数据，带有噪声等所谓的不完全数据(incomplete data)。

　　假定集合Z = (X,Y)由观测数据 X 和未观测数据Y 组成，X 和Z = (X,Y)分别称为不完整数据和完整数据。假设Z的联合概率密度被参数化地定义为P(X,Y|Θ)，其中Θ表示要被估计的参数。Θ的最大似然估计是求不完整数据的对数似然函数L(X;Θ)的最大值而得到的:

　　L(Θ;X)= log p(X|Θ) = ∫log p(X,Y|Θ)dY ;

　　EM算法包括两个步骤:由E步和M步组成，它是通过迭代地最大化完整数据的对数似然函数Lc(X;Θ)的期望来最大化不完整数据的对数似然函数，其中:

　　Lc(X;Θ) =log p(X,Y |Θ) ;

　　假设在算法第t次迭代后Θ获得的估计记为Θ(t) ，则在(t+1)次迭代时，

　　E-步:计算完整数据的对数似然函数的期望，记为:

　　Q(Θ|Θ (t)) = E{Lc(Θ;Z)|X;Θ(t)};

　　M-步:通过最大化Q(Θ|Θ(t) ) 来获得新的Θ 。

　　通过交替使用这两个步骤，EM算法逐步改进模型的参数，使参数和训练样本的似然概率逐渐增大，最后终止于一个极大点。直观地理解EM算法，它也可被看作为一个逐次逼近算法:事先并不知道模型的参数，可以随机的选择一套参数或者事先粗略地给定某个初始参数λ0 ，确定出对应于这组参数的最可能的状态，计算每个训练样本的可能结果的概率，在当前的状态下再由样本对参数修正，重新估计参数λ，并在新的参数下重新确定模型的状态，这样，通过多次的迭代，循环直至某个收敛条件满足为止，就可以使得模型的参数逐渐逼近真实参数。

　　EM算法的主要目的是提供一个简单的迭代算法计算后验密度函数，它的最大优点是简单和稳定，但容易陷入局部最优。