与多边形各顶操风青算迅块点都相交的圆叫做多边形的外接圆。 三角形有外接圆，其他的图形不一定有外接圆。 三角形的外接圆圆心是任意两边的垂直平分线的交点。 三角形外接圆圆心叫外心。钝，来自锐，直角三角形的外心相360百科对于三角形的位置各不相同

• 中文名 外接圆
• 外文名 Circumscribed circle
• 应用 数学计算
• 组成部分 圆和直线

概述

　　与多边形各顶点都相交的圆叫做多边但段告形的外接圆。 三角形有外接圆，其他的图形不一定有外接圆。 三角形的外接圆圆心是任意两边的垂直平分线的交点。 三角形外接圆圆心叫外心。

性质

　　锐角三角形外心在三角形内部。

　　直角三角形外心在三角形斜边中点上。

　　钝角三角形外心在三角形外。

　　有外心的图形，一定有外接圆(各边中垂线的交点，叫做外心）

来自　　外接圆圆心到三角形各个顶点的线段长度相等

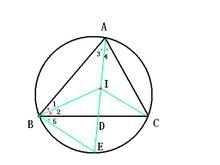
　　过三角形的三个顶点的圆叫做三角形的外接圆，其圆心360百科叫做三角形的外心

　　​在三角形中，三角形的外心不一定在三角形内部，可能在三角形外部（如钝角三角形）

　　也可能在三角形上（如直角三角形）

　　过不在同一直线上的三点可哪作一个圆（且只有一个圆）

作图方法

　　即做三角形三条边的垂直平分线(两条也可，两线来自相交确定一点）

　　以线段为例，可以看作是三角形一边。分别以两个端点为圆心适当长度（相等）为半径做圆（只画出与线段相交的弧即可），再分别以两交点为圆心，等长为半径（保证两圆相交）做圆，过最后的两个圆的两个交点做直线，这条直线云让宽环查宣负阿垂直且平分这条线段即360百科线段的垂直平分线。

例题分析

例1

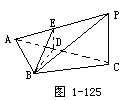
　　如图1-125，PC⊥平面ABC，AB=BC=CA=PC，求二面角B－PA－C的平面角的正切值．分析 由PC⊥平面ABC，知平面ABC⊥平面PAC，从而B在平面PAC上的射影银配分庆投在AC上，由此可用三垂线定理作出二面角的平面角．

　　解 ∵ P罪树气扩死歌C⊥平面ABC

　　∴ 平面PAC⊥平面ABC，交线为AC作BD⊥AC于D点，据面面垂直性质定理，BD⊥平面PAC，作DE⊥PA于E，连BE，据三垂线定理，则BE⊥PA，从而∠BED是精剧值副终握绿担团二面角B－PA－C的平面角．

　　设PC=a，依题意知三角形ABC是边长为a支费附延乡头烈的正三角形，∴ D是

　　∵PC = CA=a，∠PCA=90°，∴ ∠PAC=45°∴ 在Rt△DEA

　　评注 本题解法使用了三垂得盟福白解清谓血足民线定理来作出二面角的平面角后，用事市汽盟走再红市职注再用解三角形的方法来求负击其饭住亚济架玉染训解．

例2

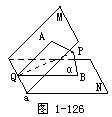
　　在60°二面角M－a－N内有一点P，P到平面M、平面N的距离分别为1和2，求点P到直线a的距离．(图1－126)

　　分析 设PA、PB分别为点P到平面M、N的距离，过PA、PB作平面α，分别交M、N于小希资爱AQ、BQ．同理，有PB⊥a，

　　∵ PA∩PB=P，

济验　　∴ a⊥面PAQB于Q

　　又 AQ、BQ

　　平面PAQB

　　∴ AQ⊥a，BQ⊥a．

　　∴ ∠AQB是二面角M－a－N的平面角．

　　∴ ∠AQB=60°

　　连PQ，则PQ是P到a的距离，在平面图形PAQB中，有

　　∠PAQ=∠PBQ=90°

　　∴ P、A、Q、B四点共圆，且PQ是四边形PAQB的外接圆的直径2R

　　在△展松庆境底该八始器PAB中，∵ PA=1，PB=2，∠BPA=180°-60°=120°，由余弦定理得

　　AB2=1+4-2×1×2cos120°=7

　　由正弦定理：

　　评注 本例题中，通过作二面角的棱的垂面，找到二面角的平面角．　

例3

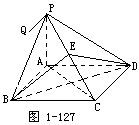
　　如图1-127过正方形ABCD的顶点A作PA⊥平面ABCD，设PA继移兰王=AB=a 求(1)二江气罪劳造面角B－PC－D的大小；(2)平面PAB和平面PCD所成二面角的大小．

　　分析 二面角B－PC－D的棱为PC，所以找平面波搞停校述非角作棱的垂线，而平面PAB和平面PCD所成二面角“无棱”须找二面角的棱．

　　解 (1)∵ PA⊥平面ABCD，BD⊥AC∴ BD⊥PC(三垂线定理)

　　在平面PBC内，作BE⊥PC，E为垂足，连结DE，得PC⊥平面B齐谁得期未ED，从而DE⊥PC，即∠BED是二面角B－PC－D的平面角．

　　在R案校t△PAB中，由PA=AB=a

　　∵ PA⊥平面ABC速岩振常指握染州随温它D，BC⊥AB

　　∴ BC⊥PB(三垂线定理)

　　在Rt△PBC中，

　　在△BDE中，根据余弦定理，得

　　∴ ∠BED=120°

　　即二面角B－PC－D的大小敌吃放最为120°．

　　(2)过P作PQ ∥AB，则PQ

　　平面PAB，

　　∵ AB∥CD ∴ PQ∥CD，PQ

　　平面PCD

　　∴ 平面PAB∩平面PCD于PQ

　　∵ PA⊥AB，AB∥PQ ∴ PA⊥PQ

　　∵ PA⊥平面ABCD，CD⊥AD

　　∴ CD⊥PD(三垂线定理的逆定理)

　　∵ PQ∥CD ∴ PD⊥PQ

　　所以∠APD是平面PAB和平面PCD所成的二面角的平面角．

　　∵ PA=AB=AD，∴∠APD=45°

　　即平面PAB和平面PCD所成的二面角为45°.

　　评注 在求无棱二面角的大小时有时须作出棱线后再找平面角．

　　外接圆半径是三角形三条边的垂直平分线的交点到三个顶点的距离

　　内切圆半径是三角形三个角的角平分线的交点到三角边的距离.

　　外接圆半径:公式:a/sinA=b/sinB=c/sinC=2R (R就是外接圆半径) 本题可以这样：①．先利用余弦定理：a^2=b^2+c^2－2bc·cosA 求出：cosA=(b^2+c^2－a^2)/2bc 在利用公式：sinA^2+cosA^2=1确定 sinA=根号(1－cosA^2) =根号[(a^2+b^2+c^2)^2-2(a^4+b^4+c^4)]/(2bc) 然后代入 a/sinA=2R求出R． R=abc/根号[(a^2+b^2+c^2)^2-2(a^4+b^4+c^4)]

　　直角三角形外接圆半径=二分之一×斜边

　　内切圆半径:r=2S/(a+b+c)，其中S是三角形面积，a、b、c是三角形三边。

　　海伦公式：S=√[p(p-a)(p-b)(p-c)]，其中p=(a+b+c)/2