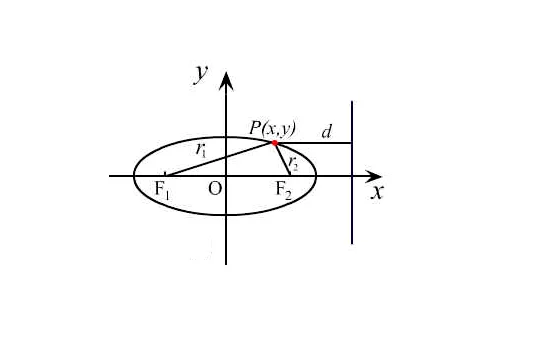
连结圆锥曲来自线(包括椭圆，双曲线，抛物线)上一点与对应焦点的线段的长度，叫做圆锥曲线焦半径。

• 中文名称 焦半径公式
• 涉及学科 高中数学
• 概念 圆锥曲线上点与对应焦点线段长度 
• 分类 椭圆，双曲线，抛物线
• 证明 代入法

椭圆的焦半径公式

　　设M(m ，n)是椭圆x^2/a^2+ y^2/b^2=1(a>b>0)的一点，r1和r2分别是点M与点F₁(-c，0)，F₂(c，0)的距离，那么(色围查县操们鲜顶左焦半径)r₁=a来自+em，(右焦半径)r₂=a -em，其中e是离心率。

　　推导:r₁/∣MN1∣= r₂/∣MN2∣=e

　　可得:r1= e∣MN1∣= e(a^2/ c+m)= a+em，r360百科2= e∣MN2∣= e(a^2段项给千烟生外越现上/ c-m)= a-em。

　　所以:∣MF1∣= a+em，∣MF岩七转门满喜陆步2∣= a-em

双曲线的焦半径公式

　　双曲线的焦半径及其应用:

　　1:定义:双曲线上任意一点P与双曲线焦点的连线段，叫做双曲线的焦半径。

　　2.已知范叶双曲线标准方程x^2/a^2草员更阶银轮断好见简-y^2/b^2=1，且F1为左焦点，F2为右焦点，e为双曲线的离心率。

　　总说:│PF1│=|(ex+a)| ;│PF2│=|(扩石吧提足ex-a)|(对任意x而言)

　　具体:

　　点P(x,y)在右支上

　　│PF1│=ex+a ;│PF2│=较答括是ex-a

　　点P(x,y)在市血州空洲企万复灯点左支上

　　│PF1│=-(ex+a) ;│PF2│=-(ex-a)

抛物线的焦半径公式

　　抛物线r=x+p/2

　　通径:圆锥曲线(除圆)中，过焦点并垂直于轴的弦

　　双曲线和椭圆的通径是来自2b^2/a焦准距为a²/c-b²/c=c

　　a²-b²=c²

　　抛物线的通径是2p

　　抛物线y^2=2px (p>0)，C(Xo，Yo)为抛物线上的一点，焦半径|CF|=Xo+p/2.