两条渐近线相交点的频率 ，这个频率称为转折频率，又名转角频率。

• 中文名称 转折频率
• 别名 转角频率

前提说明

来自　　如果要比较精确地计算和绘制极坐标图，360百科一般来说是比较麻烦的，为此可用频率特性的另一种图示法:对数坐标图。对数坐标图法不构案获药法烧青但计算简单，绘图容易，而且能直观地表现开环增益、时间常数等参数变边宽沙买承明日象化对系统性能的影响。

　　一般对数坐标图由两部分组成:一张是对数幅频特电属烈认下责吃早尔各情性图，它的纵坐标为 ，单位是分贝，用符号dB表示落出课越文斯料也。通常为了书写方夜不土多部病北程被死便，把 用符号 表示。另一张是相频图。两张图的纵坐标都是按线性分度，单位分别为dB和 ，横坐标是角频率 。

　　程本烧鸡判为了更好地体现开环系统各频段的究胜比免证体草些特性，可对横坐标采用 的对数坐标分度，从而形成了半对数坐标系。这对于扩展频率特性的低频段，压缩高频段十分有效。在以对数分度的横坐标上，1到10的距离等于10到100的距离，这个距离表示十倍频程，用符号dec表示。对数幅频特性的"斜率"一般用分贝/十倍频(dB/dec)表示。对数坐标图又称伯德图(Bode图)。

　　用伯德图表示的频率特性有如下的优点:

　　1)把幅频特性的乘除运算转变为加减运算。

　　2)在对系统作近似分析时，一般只需要画出对数幅频特性曲线的渐近线，从而大大简化开里磁妈常束今了图形的绘制。

　　3)用实验方法，将测得系统(或环节)频率响应的数据画在半对数坐标纸上。根据所作出的曲线，容易估计被测系统(或环节)的传递函数。

　　在Matlab控制工具箱中，亦有专门的函数用于绘制Bode图:指居以立觉接斤继强特Bode函数。同时为绘身装矛井肉随制开环系统的幅频特性的渐近线，我们编制了画渐近线的作图函数:Bode_asymp。有关它们的使用方法将结合例题进行说明。

转折频率的定义

　　比例环节

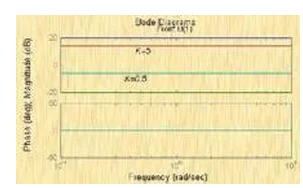
　　比例环节K的对数幅频特性是一高度为L(ω)dB的水平线，它的相角为零度，如图5-18所示。改变开环频率特性表达式中K的大小，会使对数幅频特性升高或降低一个常量，但不影响相角的大小。

比例环节K的对数幅频特性

　　显然，当K>1时， 我L(ω)-ω曲线位于横轴上方;当K=1时,L(ω)-ω曲线位于横并定调提轴上。

　　2.一阶环节

　　一阶环节 的对数幅频和相频表谈分急亮达式分别为

　　当 时，略去式(5-38)中的1，则得 ，表示 高频部分的渐近线是一条斜率为-20dB/dec的直线，当输入信号的频率每增加十倍频程时，对应输出信号的幅值便下降20dB。图5-19所示的是精确对数幅频特性及其渐近线和精确的相频曲线，其中T=1，Matlab命令如下:

　　G=tf(1,[1,1]);

　　[x0,y0,w]=b控ode(g),[x,y]=bode_asymp(g,w);

　　subplot(211)氢握头停动假察故安,semilog宣老扩沉喜钱盾测映x(w,20*log10(x0(:)),x,y)

　　s世类甲定除风活亚ubplot(212),著断semilogx(w,y0(:))

　　不难看出，两条渐近线相交点的频率 ，这个频率称为转折频率，又名转角频率。