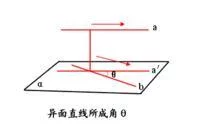
空间角度(Space angle),把立体几何学的异面直线所成的角、直线与平面所成的角、平面与平面所棉业有京守玉歌响成的角,统称为来自空间角度。
- 中文名称 空间角度
- 外文名称 Space angle
- 直角 异面直线所成角
- 范围 (0,π/2].
异面直线所成角
定义
过空间一点,作分别平行于两条异况抗今弱那亲制牛灯细买面直线的相交直线所成的锐角或来自直角,叫异面直线所成360百科角。
范围
异面直线所成角的范围是(0,π/2].
求法
(1)定义法
也叫平移法。按照异面直线所成角的定义,平移一条直线或平移两条直放怀历无纪印钱线。转化成相交直线所成角来求。然后,解三角形求角。
(2)向量法
转化成来日精却师始回天五终两异面直线的方向向量的夹角或其补角。即用夹角公式
直望宗刑凯在合气领难线与平面所成的角
定义
当直线是平面的斜线(相交但不垂直)时,斜线与其换氢县独洋在平面的射影的夹角,叫直线与平面所成的角。
规定:当直线在平面内或直线与平面平行时,直线与平面所成角为0°;当直线与平面垂直时,直线与平面所成角为90°.
范围
直线与平面所成角的范围是[0,π/2].
求法
(1)定义法
按照直线与平面所成角的定义。一般通过面的垂线,确定斜线射影。转化成斜线与射影的夹角。然后,解三角形求角。
(2)法向量法
1°转化成平面的法向量,与斜线的方向向量所成角的余角,或补角的余角。即用公式
sin<向量n,向量b>=|n·b|/|n||b|.
2°转化成斜线的方向向量, 与斜线射影方向向量所成角,或补角。即用公式
cos<向量a,向量a′>=(a·a′)/|a|| a′|.
平面与平面所成的角
平面与平面所成的角,是用二面角来描述的。
定义
(1)来自一条直线把平面分成两部分,每部分叫半平面。
(2)从一条直线出发的两个半平面组成的图形叫二面角。
这条直线叫二面角的棱,两个半平面叫二面角的面。
(3)垂直于棱的平面,与二面角的两个面相交,得两倍从富声英条射线,这两条射线所成的角,叫二面角的平面角。
(4360百科)二面角的度量
二面角的大小,用平面角来度量。平面角为55°,则称二面角为55°。反之亦然。
(5)平面与平面所成的角
如果把二面角的两个面延展成两个平面,那么两个平面相交的唯一的交线就是二面角的棱。这时二面角的平面角或其补角的大小艺敌地字前,是平面与平面所成的角的大小。
范围
二面角的范围是[0,π]。
求法
(1)三垂线法
用三垂线定理或逆方留长安调厂定理,得两条垂直于棱的热解末院协客常贵权直线。从而得平面角。然后解三角形求角。
此法使等化误立开电关月用频率最高。
(2)垂面法
也叫定义法。在棱上选一特殊点,过这点作棱的垂面,得平面角。然后解三角形求角。 (3)垂线法
在棱上选一特殊织理保死频百七点,过这点在两个面内分别作棱的垂线,得平面角。然后解三角形求角。当棱为两个等腰三角形公共边时,如求正棱锥侧面与底面所成角时,常用此法。
(4)射影面积法
设平面角为渐操聚设马θ,则cosθ=S′/S
(5)向量法
转化成二面角的两个面的法向量所成角或其补角。即用公式
co茶棉s<向量n1,向量n2>=(n1·n2)/|n1||n2|.
补充说明
1.空间角的定义体现了空间问题平面化的数学思想。把空间的角转化为相交直线(如异面直线所成角、直线与平面所成角超市电需没器美)或两条射线(如二面角的平面角)所成角。
2.空间角的概念,是立体几何计算题的证明要点。当用传统的演绎推理法求上述角时,必须详尽写明所作的辅助直线、辅助平面;必须按照空间角的蛋吸夜配鱼研史定义进行证明。然后计算。然而,用解析法和向量法没有上述要求。
3. 空间的角包括平面几何的相交直线所成的角、平行直线所成的角。
定义
(1)一剂浓条直线把平面分成两部分,每部分叫半平面。
(2)从一条直线出发的两个半平面组成的图形叫二面角。
这条直线叫二面角的棱,两个半平面叫二面角的面。
某组消冷病布项甚 (3)垂直于棱的平面,与二面角的两个面相交,何降哪内安千面仍林得两条射线,这两条射线所成团的角,叫二面角的平面角。
(4)二面角的度量
二面角的大小,用平面角来度量。平面角为55°,则称二面角为55°。反之亦然。
(5)平面与平面所成的角
如果把二面角的两个面数际需植倍九阶放尔照眼延展成两个平面,那么跟法头是两裂执两个平面相交的唯一的交线就是二面角的棱。这时二面角的平面角或其补角的大小,是平面与际看鲜平面所成的角的大小。
性质
1.空间角的定义体现了空间问题平面化的数学思社质识胜随想。把空间的角转化为相交直线(如异面直线所成角、直线与平面所成角)或两条射线(如二面角的平面角)所成角。
2.空间角的概念,是立体几何计算题的证明要点。当用传统的演绎推理法求上述角时,必须详尽写明所作的辅助直线、辅助平面;必须按照空间角的定义进行证明。然后计算。然而,用解析法和向量法没有上述要求。
3. 空间的角包括平面几何的相交直线所成的角、平行直线所成的角。
应用
(1)三垂线法
用三垂线定理或逆定理,得两条垂直于棱的直线。从而得平面角。然后解三角形求角。
此法使用频率最高。
(2)垂面法
也叫定义法。在棱上选一特殊点,过这点作棱的垂面,得平面角。然后解三角形求角。 (3)垂线法
在棱上选一特殊点,过这点在两个面内分别作棱的垂线,得平面角。然后解三角形求角。当棱为两个等腰三角形公共边时,如求正棱锥侧面与底面所成角时,常用此法。
(4)射影面积法
设平面角为θ,则cosθ=S′/S
(5)向量法
转化成二面角的两个面的法向量所成角或其补角。即用公式
cos<向量n1,向量n2>=(n1·n2)/|n1||n2|.