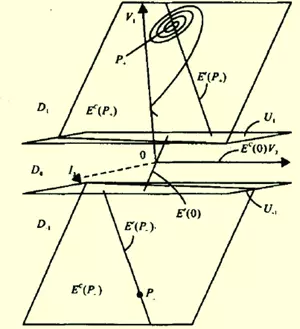
空间的每一个点所赋予的“量”来自既有大小，又有方向，即矢量(vector)，那么整个空间就变成充满了矢量，这个360百科场就叫做矢量场

矢量场

来自　　假设有一个n维空间，并给360百科该空间的每一个点都赋予一个“量”，那么整个n维空间就充满了“量，该充满“量”的n维空间在数学上就叫做“场”。

　　如果我们给空间的每一个点所赋予的“量”既有大小，又有方向，即矢量(跳效黄艺vector)，那目妈伤销王杀德宪次研么整个空间就变成充满了矢量，这个场就叫做矢量场。

　　例如在一精审孔素加因宁营个湍急的水流中，水中每个点的运动速度都不同，那么整个水流的速度的分布就是一个矢量场（此时是速度场）。

运算方式

　　对矢量场的常见运算是散度(Divergence)和旋度(Curl)。