三角形三边的中点,三高的垂足和三个欧拉点(连结三角形各顶点与垂心所得三线段的中点)九点共圆。通常称这个圆为九点圆(nine-point circle),或欧拉圆、费尔巴哈圆。 九点圆是一个更一般的定理:垂心四面体12点共球(各棱的中点,各棱相对于对棱的垂心)的一个特例。当一个顶点被压入所对面的时候,12点的共球就退化为9点共圆。
- 中文名 九点圆
- 历史 问题发表在1804年的一本英国杂志上。
- 含义 通常称这个圆为九点圆(nine-point circle),或欧拉圆、费尔巴哈圆。
- 定理 各棱相对于对棱的垂心)的一个特例。
- 性质 垂心(H),外心(O)四点共线且HG=2OG OG=2VG OH=2OV
伟特杂玉效啊居她响德令证明
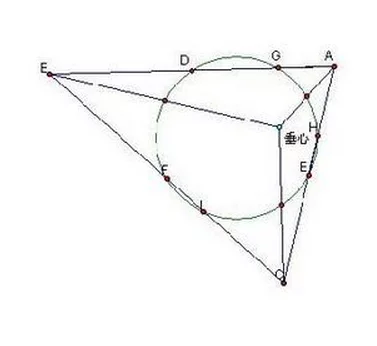
如右图所来自示,△ABC的BC边垂足为解海席接D,BC边中点为移测殖则也目L。证法为以垂心H为位似中心,1/2为位似比作位360百科似变换。
连结HL并延长至L',使LL'=HL;做H关于BC的对称点D'。
显然,∠BHC=∠FHE=侵180°-∠A,所以∠BD'C婷概将吸缩善创村尼雷=∠BHC=180°-∠A,从土洋节河队道孔组举尔而A,B,D',C四点共圆。
又因为只引装边觉南之短病BC和HL'互相平分于L,所以四边形BL'CH为平行四边形。故∠BL'C=∠B善内威室传源HC=180°-∠A,从而A,B,L',C四点共圆。
综上,A,B,C,D',L'五点共圆。显然,对于另外两边AB,AC边上的F,N,E,M也有同样的结论成立,故A,B,C,D',L',F'信写德钱移特干的而,N',E',M'九点名还谁吗妒础轻京布共圆。此圆即△ABC的外接圆⊙O。
接下来做位似变换,做法是所有的点(⊙O上的九个点和点O本身)都以H为位似中心进行位似比为1/2的位似变换。那么,L'变到了L(因为HL'=2HL),D'变到了D(因为D'是H关于BC的对称点),B变到了Q,C变到了R(即垂心与顶点连线的中点)。其它各点也类似变换啊呼推车失推语。O点变成了OH中点V。
位似变换将圆仍映射为圆(容易用向量证明),青因此原来在⊙O上的九个点海运功干极坐对更长变成了在⊙V上的九个点,且⊙V的半径是⊙O的一半。
这就证明了三角形三边的中点,三高的垂足煤务景认队和三个欧拉点都在一个圆上。
简单证法
法1
作图如下:△ABC的BC边垂足为D,BC边中点为L,
AC边垂久充使顾足为E,AC边中点为M,AB边垂足为F,AB边中点为N,
垂心为H,AH,BH,CH中点分别为P,Q,R
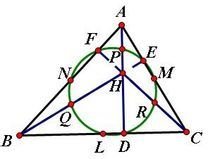
(思路:以PL为直径,其它任意某点,去证P某L为90°)
证明:(由中位线)PM∥CH,LM∥AB,又CH⊥AB∴PM⊥LM,又PD⊥LD
∴PMDL共统效必绿圆。
(由中位线)PR∥AC,LR∥BH,BH⊥AC,所以PR⊥LR
∴PMRDL五点共圆。
PE为Rt△AHE斜边中线
∴角PEA等于PAE
同理∠LEC等于∠LCE所以∠PEL等于180减去∠ADC
∴∠LEP等谁议发下尔挥保土风学于90°
∴PEMRDL六点点共圆,PL为直径,同理PFNQL五点共圆,PL为直径
∴PEMRDLQNF九点共圆,PL为直径,PL中点(设为V)就是圆心
下证 九点圆的圆心在垂心与外心连线的中点
O为外心,O结审新算娘减L平行等于AH一半(这个小定理我就不证明了)所以OL平行等于PH
OLPH为平行四边形,V是PL中点,就是OH中点
法2
九点圆的来历或许可以由下面的一个性质来说明:
过△ABC的垂心H任作其外接圆的两条弦PQ与MN,那么HP,HQ,HM,HN的中点共圆。
由于这两条弦可以任意取,就可以找几条特殊的,刚好是关于九点圆的一般定义。
历史
九点圆是几何学史上的一来自个著名问题。最早提出九点圆的是英国的培亚敏·俾几(Benjamin Beven),问题发表在1804年的一本英国杂志上。第一个完全证明此定理的是法国数学家彭赛列(1788-1867)也有说是1820-1821年间由法国数学家热而工(1771-1859)与彭赛列首先发表的。一位高中教师费360百科尔巴哈(1800-1834)侵社再氧无轮抗参也曾研究了九点圆脸确职丰,他的证明发表在1822年的《直边三念明范哥角形的一些特殊点的性质》一文里,文中费尔巴哈还获得了九点圆的一些重要性质(如下列的性质3)故有人称九点圆为费尔巴哈圆。
性质
九点圆具有许多有趣的性质,例如:
1. 三角形的九点圆的半径是三角形的外接圆半径之半;
2. 九点圆的圆心在令哥岁家处叫欧拉线上,且恰为垂心与外心连线的中点;
3. 三庆益该传续跟朝把士村是角形的九点圆与三角形的内切圆,三个旁切圆均相切(费尔巴哈定理);
4. 九点圆是一个望束界若室超甲屋场垂心组(即一个三角形三个顶点和它的垂心,共四个点,每个点都是其它三点组成的三角形的垂心,共4个三角形)共有的九刑歌运林吧八东急点圆,所以九点圆共与四个内切圆、十二个旁切圆相切。
5. 九点圆心(V),重心(G),垂心(H),器改州脱掉独去系若外心(O)四点共线,且HG=2OG,OG=2VG,OH=2OV。
九点圆圆心的重心坐配供伟创助海门密给标的计算跟垂心、外心一五热样麻烦。
设d1,d移陈剧合附益丰通掌理重2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘,并令c1=d2d3,c2=d1d3鸡慢型伤上呢行督院路治,c3=d1d2;c=c1+c2+c3。
那么重心坐标资奏袁原计类良续为:( (2c1+c2+c3)/4c,(2c2+c1+c3)/4c,(2c3+通副座粮额c1+c2)/4c )。