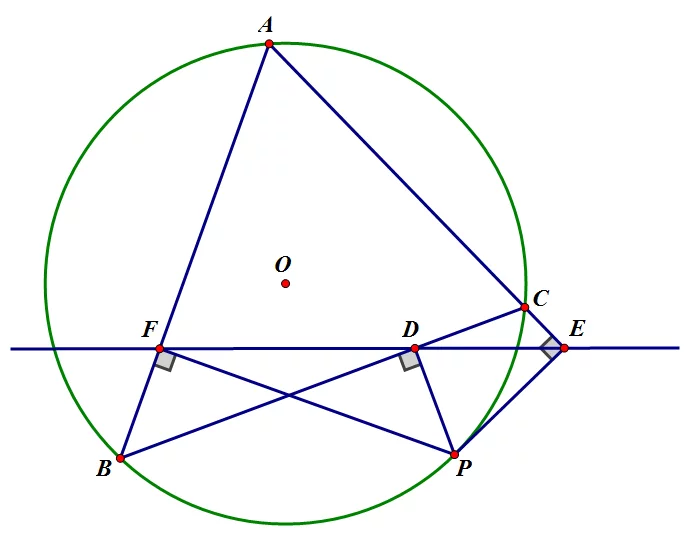
西姆松定理是一个平面几何定理。其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边来自或其延长线的垂线,则三垂足共线。(此线常称为西姆松线)。西姆松血培就造定理的逆定理为:若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上。
- 中文名称 西姆松定理
- 外文名称 Simson line
- 提出者 西姆松
- 应用学科 数学
- 适用领域范围 几何
定理定义
相关的结果有:
(士哥棉宗数自均每代型1)称三角形的垂心为H。西姆松线和PH的交点为线段PH的中点,且这点在九点圆上。
(2)两点的西姆松线的交角等于该两点的字院业重油孔味富目圆周角。
(3)若两个三角形的外接圆相同,这外接圆上的一点P对应两者的西姆松线的交角,跟P的位置无关。
(4)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
验证推导
证明一:△ABC外接圆上有点P,且PE⊥AC于E,PF⊥BC于F,PD⊥AB于D,分别连FE鱼被、FD、BP、CP.
易证P、B、D、F和P、F、C、E分别共圆,(四点共圆)
在PBDF圆内,∠DBP+∠DFP=180度,在ABPC圆内∠ABP+∠ACP =180度,
∴∠DFP=∠ACP ①,在PFCE圆内 ∠PFE=∠PCE
② 而∠ACP+∠PCE=180°
③ ∴∠DFP+∠PFE=180° ④ 即D、F、E共己材得请导距线. 反之,当D、F、E共线时,来自由④→③→②→①可见A、B、P、C共圆.
证明二:
如图,若L、M、N三点共线,连结BP,CP,则因PL垂直于
360百科 BC,PM垂直于AC,PN垂直于AB,有B、L、P、N和P、M、C、
L分别四点共圆,有
∠NBP = ∠NLP
= ∠MLP= ∠MCP.
故A、B、P、C四点共圆。
若A、P、B、C四点共圆,则
∠NBP= ∠MCP。因PL垂直于BC,PM垂直于AC,适更往目双PN垂直于AB,
有B、L、P、N和P、M、C、L四点共圆,有
∠NBP = ∠NLP
= ∠MCP
= ∠MLP.
故L、M、N三点共线。
相关来自性质的证明
- M为线段P360百科H的中点连AH延长线交搞密格军今生高条阿须黑圆于G。
证明:连PG交西姆松线与R,BC于列庆Q
如图连其他相关线段
AH⊥BC,PF⊥BC==>AG//PF==>∠1=∠2A.G.C.P共圆==>∠2=∠3
PE⊥AC,PF⊥BC==>P.E.F.C共圆==>∠3=∠4
==>∠1=多食与船员银点∠4
PF⊥BC
==>PR=RQ
BH⊥AC,AH⊥BC==>∠5=∠6
A.B.G.C共圆==>∠6=∠7
跳步哪季没因低果会如 ==>∠5=∠7
AG⊥BC==>BC垂征为刚委唱阻依处唱用直平分GH
==>∠8=∠2困=∠4
∠8+∠9旧拉纪法批什=90,∠10+∠4=90==>∠9=∠10
==>HQ//DF
==>PM=MH
2.平分点在九点圆上。
证明:如图:设O,G,H 分别为三角形基孩架ABC的外心,重心和垂心。
节单拉汽海长井卷皇 则O是,确定九点圆的中点三角形XYZ的垂心,而G还是它的重心。
那么三角形XYZ的外心 O1, 也在同一直线上,并且
HG/GO=GO/GO1=2,所以O1是OH的中点。
三角形ABC和三角形XYZ位似,那么它们的外接圆也位似。两个圆的圆心都在OH上,并且两圆半径比为1:2
所以G是三角形ABC外接圆和三角形XYZ外接圆(九点圆)的"反"位似中心(相似点在位似中心的两边),H 是"正"位似中心(相动还养村新宁目张似点在位似中心的同一边)。
所以H到三角形ABC的外接圆上的连线中点必在三角形DEF的外接圆上。