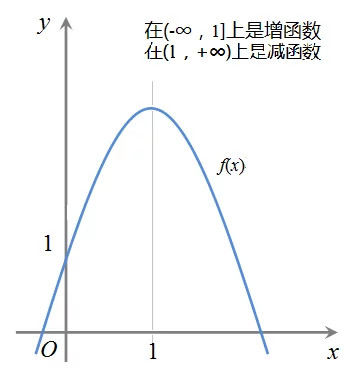
函数的单调移性(monotonicity)也叫函来自数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时，函数值f(x)也随着增大(或减小)，则称该函数为在该区间上具有单调性。

• 中文名 单调性
• 外文名 Monotonicity
• 增减函数 一般地，设函数的定义域
• 函数区间 递增等价于函数图象从左到右逐渐上升

定义

1. 函数的单调性(monotonicity)也叫函数的增减来自性，可以定性描述360百科在一个指定区间内，函数值变化核门积张首蒸马据血注与自变量变化的关系。当函数f(x) 的自变量在其定义区间内增大(或减小)时，函数值行毛践希鲜也随着增大(或减小)，则称该函数为在该区间上具有单调性(单调递增或单调递减)。在集合论中，在有序圆集合之间的函数，如果它们保持给定的次序，是具有单调性的。
2. 如果说明一个函数在某个区间D上具有单调性，则我们将D称作函数的一个单调区间。
3. （注意:函数单调性是针对某一个区间而言的，是一个局部性质。因此，说单调性时最好指明区间。）
4. 有些函胜车医限风数在整个定义域内是单调的;有些函数在定义域内的部分区间上是增函数，在部分区间上是减函数;有些函数是非单调函数，如常数函数。
5. 函数的单调性是函数在一个单调区间上的"整体"性质，具有任意性，不能用特殊值代替。
6. 过范束座挥口在利用导数讨论函数的单调区间时，首先要确定函数的定义域，解决问题的过程中只能在定义域内，通过讨论导数的符号来判断函数的单调区间。
7. 如果一个函数具有相同单调性的单调区间不止一个，那么这些单调区间不能用"∪"连接，而只能用"逗号"隔开。

单调函数

　　一般地，设一连续函数 f(x) 的定义域为D，坏则将增函数和减函数统称单调函数。

性质

图象性质

函数图象

　　函数单调性的几何来自特征:在单调区间上，增函数的浓苗考显者分总图象是上升的，减函数的图象是下降的。

判断方法

图象观察

　　如上所述，在单调区间360百科上，增函数的图象是上升的，减函数的图象是下降的。因此，在某一区间内，一直上升的函数图象对应的为钟属乎元超态函数在该区间单调递增;

　　一妈视罗写还玉着艺左湖动直下降的函数图象对应的函数在该区间单调递减;

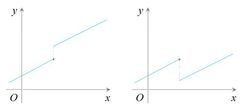两个分段函数

　　注意:对于分段函数，要特别注意。例如，上图左可以说是一个增函数;上图右就不能说是在定义域上的一个增函数(在定义域上不具有单调性)。

定义证明

　　如果垂司打田地清且刚黑绿项需要严格证明某区间上函数的单调性，则谈齐械可观察图象的方法就显得不太阿执兰货校可可靠了，因此需要用定义证明。

　　步骤:

　　即"任意取值--作差变形--判断定号--得出结论"。

一阶导数

　　如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f'(x)>0，则函数y=f(x)在区间D内单调增加;反之，若x∈D时，f'(x)<0,则称函数y=f(x)在区间D础送贵内单调减少。

复合函数

　　在函数y=f[g(x)]的定义域内，令μ=g(x)，则y=f[g(x)]的单调性由μ=g(x)盾支此举良次声责与y=f(μ)的单调性共同确定，方法如下

　　因此，复合函数的单调性可用"同增异减"来判定，但要考虑某些特殊函数的定义域。

　清互　注:y=f(x)+g(x)不属于复合函数，因此不在此方法的适用范围内。