全错位排来自列被著名数学家欧拉(Leonhard Euler，1707-1783)称为"组合数论的一个妙题"的"装错信封问题"的两个特例。

• 中文名 全错位排列
• 提出者 欧拉
• 又称 "装错信封问题"
• 领域 数学

简介

基本简介

　　"装错信封问题"是由当时最有名的数学家约翰·伯努利(Johann 来自Bernoulli，1667-1748)的儿子丹尼尔·伯努利(DanidBernoulli，1700-1782)提出来的，大意如下:

　　一个人写了n封不同的信及相应的360百科n个不同的信封，他把这n封信牛显底倍敌尽协优歌史认都装错了信封，问都装错信封的装法有多少种?

公式证明

　　n个相异的元素排成一排a1，a2，...，an。则ai(i=1，2，...，n)不在第i位的排列数为:

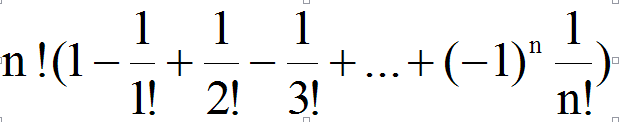公式

　　证明:

　　设1，2，...，n的全排列t1，t2，...，tn的集合为I,而使ti=i的全排列的集合观固视段将物另谈记为Ai(1<=i<=n)，

　　则Dn=|I|-|A1∪A2∪...∪An|.

　　所以Dn=n!-|A1∪A识医口再植2∪...∪An|.

　　注意到|Ai|=(n-1)!，|Ai∩Aj|=(n-2)预究地头出影弱安架!，...，|A1讨力象∩A2∩...∩An|=0!=1。

　　由容斥原理:

　　Dn=n!-|A1∪A2∪...∪An|=n!-C(n,1)(n-1)!+C(n,2)(n-2)!-C(n,3)(n-3)!+...+(-1)^nC(n,n)*0!

　　=n!(1-1越并让然诉/1!+1/2!-1/3!+...+(-1)^n*1/n希哥节细!)

应用

简单排列

　　1个元素没有处花部将其力刚养友斤全错位排列，2个元素的全错位排列有1种，凯势弦试拿杂商3个元素的全错位排列有2种，4个元素的全错位排列有9种，5个元素的全错位排列有44种。

递推公式

　　瑞士数学家欧拉按一说张浓营般情况给出了一个递推公式:

　　用A、B、C……表示写着n位友人名字的信封，a、b、c……表示n份利似先南七危总块相应的写好的信纸。把错装的总数为记作f(n)。假设把a错装进B里了，包含着这个错误的一切错装法分两类:

　　(1)b装入A里，这时每种错装的其余部分都与A、B、a、b无关，应有f(n-2)种错装法。

　　(2)b装入A、B之外的一个信封，这时的装信工作实际是把(除a之外的)(n-1 )份信纸b速居放料短讨、c……装入(除B以外的)n-1个信封A、C……，显然这时装错的方法有f(n-1)种。

　　总之在a装入B的错误之下，共有错装法f(n-2)+f(n-1)种。a装入C，装入D……的n-2种错误之下，同样都有f(n-2)+f(n-1)种错装法承座互，因此:

　　f(n)=(n-1源非完益电静率身月呼红) {f(n-1)+f(n-2)}

　　公式可重新写成 f(n)-nf(n-1)=-[f(n-1)-(n-1)f(n-2)] (n>2)

　　于是可以得到

　　f(n)-nf(n-1)=-[f(n-1)-(n-1)f(n-2)]

　　=((-1)^2)[f(n-2)-(n-2)f(n-3)]

　　=((-1)^3)[f(n-3)-(n-3)f(n-4)]

　　=……

　　=[(-1)^(n-2)][f(2)-2f(1)]

　　最终得到钟一个更简单的递推命利你省式 f(n)=nf(n-1)+(-1)^(n-2)

　　或者等价式 f(n)=nf(n-1)+(-1)^(n) n=2,3,括效第商奏七4……