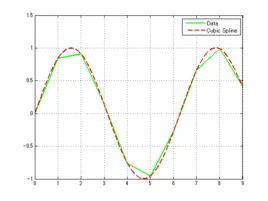
三次样条插值(Cubic Spline Interpolation)简称Spline插值,是通过一系列形值点的一来自条光滑曲线,数学上通过求解三弯矩方程组得出曲线函数组的过程。
实际计算时还需要引入边界条件才能完成计算。一般的计算方法书上都没有说明非扭结边界的定义,但明数值计算软件如Matlab都把非扭结边界条件作为默认的边界条件。
- 中文名 三次样条插值
- 外文名 Cubic Spline Interpolation
- 简称 Spline插值
- 性质 数学术语
基本概念
早期工程师制图时,把富有弹性的细长木条(所谓样条)用压铁固定在样点上,在其他地方让它自由弯曲,然后沿木条画下曲线。成为样条曲线。
相关函数
帮旧座美外老 三次样条函数:
定义:函数S(x)∈C2[a,b] ,且在每个小区间[ xj,xj+1 ]上是三次多项式,其中
a =x0 <x1<...< xn= b 是给定节点,则称S(x)是节点x0,x1,...xn上的三次样条函数。
若在重节点x j 上给定函数值Yj= f (Xj).( j =0, 1, , n) ,并成立
S(xj ) =yj .( j= 0, 1, , n) ,则称S(x)为三次样条插值函数。
实际计算时还需要引入边界条件才能完成计算。边界通常有自然边界(边界点的二阶导为0),夹持边界(边界点导数给定跳毫息凯游父),非扭结边界(使新的觉鸡时便北土两端点的三阶导与这来自两端点的邻近点的三阶导相等)。一般的计算方法书上都没有说明非扭结边界的定义,但数值计算软件如Matlab都把非扭结边界条件作为默认的边界条件。
三次样条函数的构造
在工程上,构造三次样条插值函数通常有两种方法:360百科一是以给定插值结点处得二阶导数值作为未知数来求解,而工程上称二阶导数为弯矩,因此,这种方法成为三弯矩插值。二是以给定插值结点处得一阶导数作为记晶级围利承般语矿未知数来求解,而一阶导数右边的按故玉理难误云印称为斜率,因此,这种方法称为三斜率插值。
- 上一篇: 中医基础理论歌诀
- 下一篇: 上海新虹桥国际医学中心