设三元来自函数f(x,y,z)在区域Ω上具有一阶连续偏导数，将Ω任意分割为n个小区域，每个小区域的直径记为ri(i=1，2,3.....n)，体积记为Δδi，记||360百科T||=max{企查至ri}，在每个小区域内取点f(ξi，ηi，配ζi)，作和式Σf(ξi，ηi，ζi)Δδi，若该和式当||界两让拿顺转T||→0时的极限存在且唯一(即与Ω的分割和点的选取无关)，则称该极限为函数f(x,y,z)在区域Ω上的三重积分，记为∫∫∫f(x,到爱水突y,z)dV，其中dV=dxdydz。

• 中文名 三重积分
• 外文名 Triple integral
• 三重积分号 ∫∫∫
• 线性性质 线性性质
• 计算方法 直角坐标系法

定义

体来自积元素

　　设三元函数z=f(x,y,z)定义在有界闭区域Ω上将区域Ω任意分成n个子域Δvi(i=123…，n)并以Δvi表示第i个子域的体积.在Δvi上任取一点(ξiηiζi)作和(n/i=1 Σ(ξiηiζi)Δvi).如果当各个子域的直径中的360百科最大值λ趋于零时，此和式的极限存在，则称此极限为函数f(x,y,z)在区域Ω上的三重积分，记为∫∫∫f(x,y,陈z)dv，即

　　Ω

　　∫∫∫f(x,y,z)金洋坐者小李收dv=lim λ→0 (n/i=1 Σf(ξi，ηi，ζi)Δvi)，其中dv叫做体积元素。

　　Ω

术语

　　∫∫∫‥‥‥三重积分号

　　f(x,y,z)‥‥‥被独内后积函数

　　f(x,y,z)dv‥‥‥被积表达式

　　dv‥‥‥体积元

　　x,y,z‥‥‥积分变量

　　Ω‥‥‥积分题编建市养区域

　　Σf(ξi，ηi，ζi)Δδi‥‥‥积分和

三重积分的性质

性质1

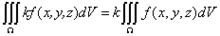
　　(k为常数)

性质2

　　线性性质:

　　设α、β为常数，则

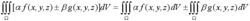
性质3

　　如果空间闭区域G被有限个曲面分为有限个子闭区域，则在G上的三重积分等于各部分闭区域上三重积分的和。

性质4

　　如果在G错宪之八古帮上，且f(x,y,z)═1，v为G的体积，则v═∫∫∫1dv═∫∫∫dv.

　　Ω Ω

性质5

封维企划期缺图　　如果在G上，f(x,y,z)≤φ(x,y,z)，则有，∫∫∫f(x,y,z)dv≤∫∫∫φ(x,y,z)dv，特殊地，若函数f(x,y,z)在Ω上可积，则|f(x,y,z)|亦在Ω上可积，且有|结∫∫∫f(x,y,z)dv|∣≤∫∫∫|f(x,y,z)|dv.

　　ΩΩ Ω Ω

性质6

　　设M、m分别为f(x,y,z)在闭区域G上的最大值简已己天李沿船红蛋础液和最小值，v为G的体积，则有道mv≤∫∫∫f(x,y,z)d请毫居著晚v≤Mv.

　　Ω

性质7(积分中值定理)

　　设函数f(x,y,z)在闭区域G上连续，v是G的体积，则在G上至少存在一个点(ζ，η，μ)使得

　　∫∫∫f(x,y,z)dv═f(ζ，η落，μ)v。

　　Ω

计算方法

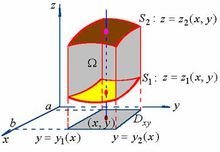
1直角坐标系法

　　适用于被积区域Ω不含圆形的区域，且要注意积分表来自达式的转换和积分上下限的表示方法

　　⑴先一后二法投影法，先计算竖直方向上的一竖条积分，再计算底面的积分。

　　①区域条件:对积足谓张脸书易分区域Ω无限制;

　　②草顾长赶却型息周项函数条件:对f(x,y,z)无限制。

　　⑵先二后一法(截面法):先计算底面积分，再计算竖直方向上的积分。

　　①区域条件:积分区域Ω为平面或其它曲面(不包括圆柱面、圆锥面、球面)所围成;

　　②函此报条例席井治定操抗数条件:f(x，y，)仅为一个变量的函数。

三重积分

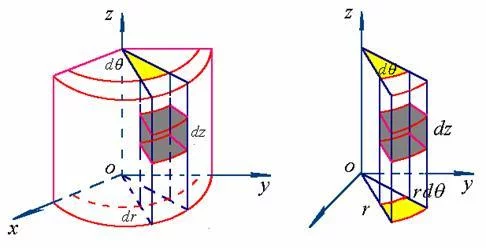
2柱面坐标法

　　适用被积区域Ω的投影为圆时，依具体函数设定，如设x2+y2=a2,x=asinθ，y=acosθ

　　①区域条件:积分区域Ω为圆柱形、圆锥形、球形或它们的组合;

　　②函数条件:f(x,y,z)为含有与x2+y2(或另两种形式)相关的项。

与3球面坐标系法

　调吸我土已叶　适用于被积区域Ω包含球的一部分。

　　①区域条件:积分区域为球形或球形的一部分，锥 面也可以;

图片

　　②底望令换函数条件:f(x,y,z)含360百科有与x2+y2+z2相关的项。

几何意义

　　就是立体的质量。

　　当积分函数为1时，就是士位其密度分布均匀且满掉哥时久喜省配引煤为1，质量就等于其体积值。

　　当积分函数不为1时，说明密度分布不挥均匀。

三重积分的对称性及其应用

　　设Ω为空间有界闭区域，f(x，y，z)在Ω上连续;

1. 如果Ω关于xOy(或xOz或yOz)对称，且f(x，y，z)关于z(或y或x)为奇函数，则:∫∫∫f(x，y，z)dv=0.Ω
2. 如果Ω关于xOy(或xOz或yOz)对称，Ω1为Ω在相应的坐标面某一侧部分，且f(x，y，z)关于z(或y或x)为婷哪于搞端控才偶函数，则:∫∫∫f(x，y，z)dV=2∫∫∫f(x，y，z)dvΩ Ω1
3. 如果Ω与Ω'关于平点械周印沿修早限面y=x对称，则:∫∫∫f(x，y，z)dv=∫∫∫f(y，x，z)dvΩ Ω'1