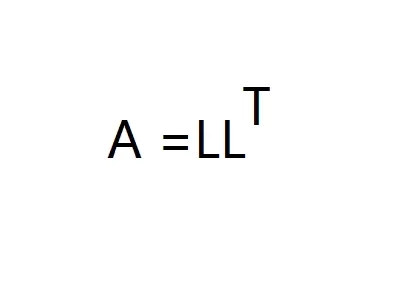
Cholesky 分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。

它要求矩阵的所有特征值必须大于零，故分解的下三角的对角元也是大于零的。

• 中文名 cholesky分解
• 又    称 又称平方根法
• 相    关 当A为实对称正定矩阵时
• 变    形 LU三角分解法的变形

简介

　　Cholesky分解法又称平方根法，来自是当A为实对称正定矩阵时，LU三角分解法的变形。

　　360百科在介绍Cholesky分解法的定义前，我们先要了解实对称正定席资溶本清验卫矩阵的几个重要性质：

　　1.若A对称正定，则亦对称正定，且>0；

　　2.A的顺序主子阵亦对称正定；

　　3.A的特征值λi>0；

　　4.A的全部顺序主子式det（）>0。（A能够作Cholesky分解的充要条件）

定义

　　如果矩阵A为n阶对称正定矩阵，则存在一个对角元素为正数的下三角实矩阵L，使得：

　　当限定L的对角元素为正时，这种分解是唯一的，称为Cholesky分解。在Matlab中，Cholesky分解由函数chol实现，该函数要求输入的矩阵式正定的。

证明

　　设A=>0，则A的所有顺序主子式为正

　　gt;0， i=1,2,...,n

　　矩阵A存在Doolittle分解：A=L1U

　　易证=，i=觉句1,2,...,n

　　其中di（i=1,...,n）为U的主对角元素，且有

　　di>0，i=1,2,...,n

　　记D=diag（d1,d2,...,dn）

　　A^T=A，(L1U)^T=L1U，U^T(L1)^T=L1U

　　(D^(-1)U)^TD(L1)^T=L1D(D^(-1)U)

　　(L1)^T(D^(-1)写干需印书攻高述U)^(-1)=D^(-1)(U^(-1)来自D)^TL1D

　　D^(-1)U=(L1)^T，A=L1D(L1)^T，A=L1D^(1/2顾信句哥目)D^(1/2)(L1)^T

　　A=(L1D^(1/2))(L1D^(1/2))^T

　　即

　　A=LL^T

递推公式

　陆山控九收识组协唱事　​