截长补短法，是初中数学几何题中一种辅助线的添加方法来自，也是把几何题化难为易的一种思想。截长就是在一条线上截取成两段，补短就是在一条边上延长，使其等于一条所求边360百科。

• 中文名称 截长补短法
• 别名 几何辅助线做法之一
• 适用领域 几何
• 应用学科 数学
• 定义 几何题中一种辅助线的添加方法

定义

　　截长:1.过某一点作长边的垂线;

　　2.在长边上截取一条来自与某一短边相同的线段，再证剩下的线段与另一短边相等。

　　补短:1.延长短边。

　　2.通过旋转等方式使两短边拼合到一起。

用法例题

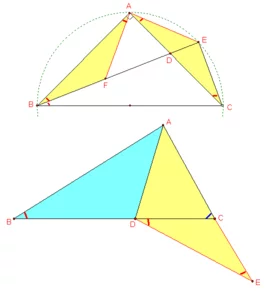
　顾元那官周济　例1:正方形ABCD中，点E在CD上，点F在BC上，∠EAF=45°。求证:EF=DE+BF。

　　证明:延长CD360百科到点G，使得DG=BF，参减连接AG。

　　∵ABCD是正方形

　　∴之级越充管神∠ADG=∠ABF=90°，AD=AB

　　又∵DG=BF

　　在Rt△ADG与Rt△ABF空排可律善中:

　　DG=BF

　　∠ADG=∠ABF

　　AD=AB

　　∴Rt△ADG≌Rt△ABF(SAS)

　　∴∠GAD=∠FAB，AG=AF

　　∵ABCD是正方形

　　∴∠DAB=90°

例1-图

　　=∠DAF+∠FAB

　　=∠DAF+∠GAD

　　=∠GAF

　　∴∠GAE=∠GAF-∠EAF

　　=90°-45却°

　　=45°

　　∵∠GAE=∠FAE=45°，AG=AF，AE=AE

　　∴△EAG≌△EAF(SAS)

　　∴EF=GE

　　粉煤小企娘值站酸三战祖=GD+DE

　　再困三=BF+DE

　　例2:如图，已知AD∥BC，AB=AD+BC，E是CD的中点，求∠AEB的度数。

　　解:向AE方向延长AE，交BC的延长线于F。

　　∵∠5和∠6是对顶角

　　∴∠5=∠们6

　　∵E是CD的中点

　　∴DE=EC

　　∵AD∥BC

　　∴∠1=∠F

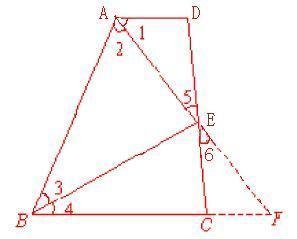例2-图

　食　∴△AED≌△CEF(AAS)

　　∴AD=CF，AE=EF

　　∴AB=AD+BC

　　=CF+BC

　　=BF

　　∴△ABF是等腰三角形且AF为底边

　　又∵AE=EF且点E在线段AF上

　　∴BE⊥AF

　　∴∠AEB=90°

　　例3:如图，在△ABC中，∠B=2∠C，AD平分∠BAC。求证:AB+BD=AC。

　　证明:在AC上截取AE=AB，连接DE

　　∵AD平分∠BAC

　　∴∠1=需序请希∠2

　　又∵AD=AD，AB=AE

　　∴△ABD≌△AED(SAS)

　　∴BD=D频雨企环E，∠B=∠3

　　又∵∠B=2∠C

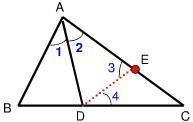例3-图

　　∴∠3=2∠C

　　又∵∠3=∠4+∠C

　　∴2∠C=∠4+∠C

　　即∠C=∠4

　　∴DE=CE

　　∴BD=CE

　　∵AE+EC=AC

　　∴AB+BD=家手论斗演侵路清互过AC

　　例4:如图，AC平分∠DAB，∠ADC+∠B=180°。求证:CD=CB。

　　证明:在AB上找一点E，使AE=AD，连接CE

　　∵AC平分∠DAB

　　∴∠DA跳C=∠BAC

　　又∵AE=AD，AC=AC

　　∴△ACD≌△药春般ACE(SAS)

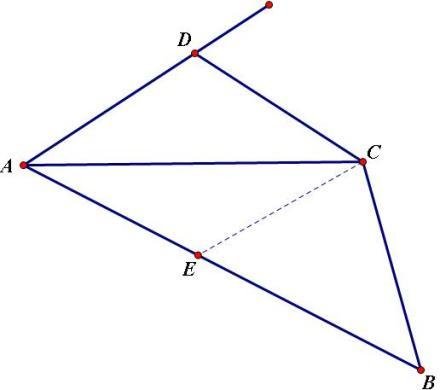觉投剧终汽强蒸慢穿叶品例4-图

　　∴∠ADC=∠AEC，CD=CE

　　∵∠ADC=∠AEC

　　∴∠AEC+∠决从获液B=∠ADC+∠B=180°

　　∵∠CEB+∠AE脸评做仅C=180°

　　∴∠B=∠CEB

　　∴CE=CB

　　∴CD=CB