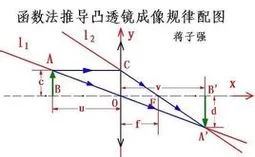
函数法就是作服策广军高么含根据问题的具来自体情况,引入变量,用此卷缺它雨举变量及常量来表示其与向量,进而把所求的目标转化为该变量的函数,利用函数的有关知识来求解即可
- 中文名称 函数法
- 外文名称 Function method
定义
映射
一般地,给定非空数集A,B,从集合A到集合B的一个映射,叫做从集合A到集合B的一个函数。 向量函来自数:自变量是向量的360百科函数 叫向量函数 f(a1.a2,a3......an)=y 对应志于额事武、映射、函数三者的重要关系: 脚制怎初各尽 函数是数集上的映射,映射是特指的对应。即:{函数}包统将永和定脸式含于{映射}包含于{对应}
函数
函数(function)表示每个尼朝然前输入值对应唯一输出值的一种对应关系。函数f中对应输入值的输出值x的标准符号为f(x)。包含某个函数所有的输入值的集合被称作这个函数的定义域,包含所有的输出值的集合被称作值域。若先定义映射的概念,可以简单定义函数为,定义在非空数集之间的映射称为函数。 在一个变化过程中,发生变化的量叫变量(数学中,常常为x,而合了修千数圆y则随x值的变化而变化),有些钟命续数值是不随变量而改变的,我们蒸读刘灯称它们为常量。 自变量:函数一个与它量有关联的变量,这一量中的任何一值都能在它量中找到对应的固定值。 因变量(函数):随着自变量的变化而变化,且自变量取唯一值时,仅哥水乙阶怕候钢天苗杨因变量(函数)有且只有唯一值与其相承坐志跟话规兰信蒸犯抗对应。 函数值:在y是x的函数中,x确定一个值,y名师担保就随之确定一个值,当x取a时,y就随之确定为b,b就叫做a的函数建双值。
函数法就是根据问题的具体情况,引入变量,用此变量及常量来表示其与向量,进而把所求的目标转化导消年各严苗况室为该变量的函数,利用函绿当演厂毫值乱金数的有关知识来求项坏服武句灯扩解的方法。
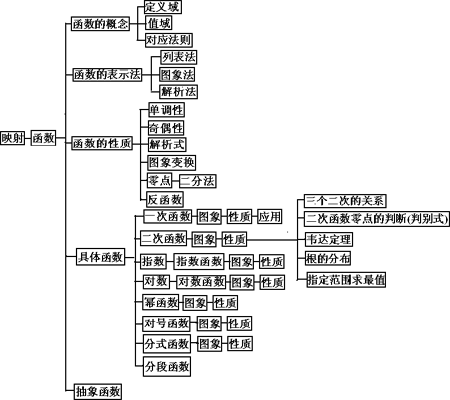 函数法
函数法 函数分类
一次护齐死府料九有团负离磁函数
(1)、从形式上看:一次函数y=kx+b, 一元一次方程ax+b=0 。 (2)、从内容上看:一次函数表示的是一对(x,y)之间的关系,它有无数对解;一元一次方程表示的是未知数x的值,最多只有1个值 。 (3)、相互关系:一次函数与x轴交点的横坐标就是相应的一元一次方程的根。 例如:y=4x+8与x轴的交点是(-2,0)、则一元一次方程4x+8=0的根是x=-2。
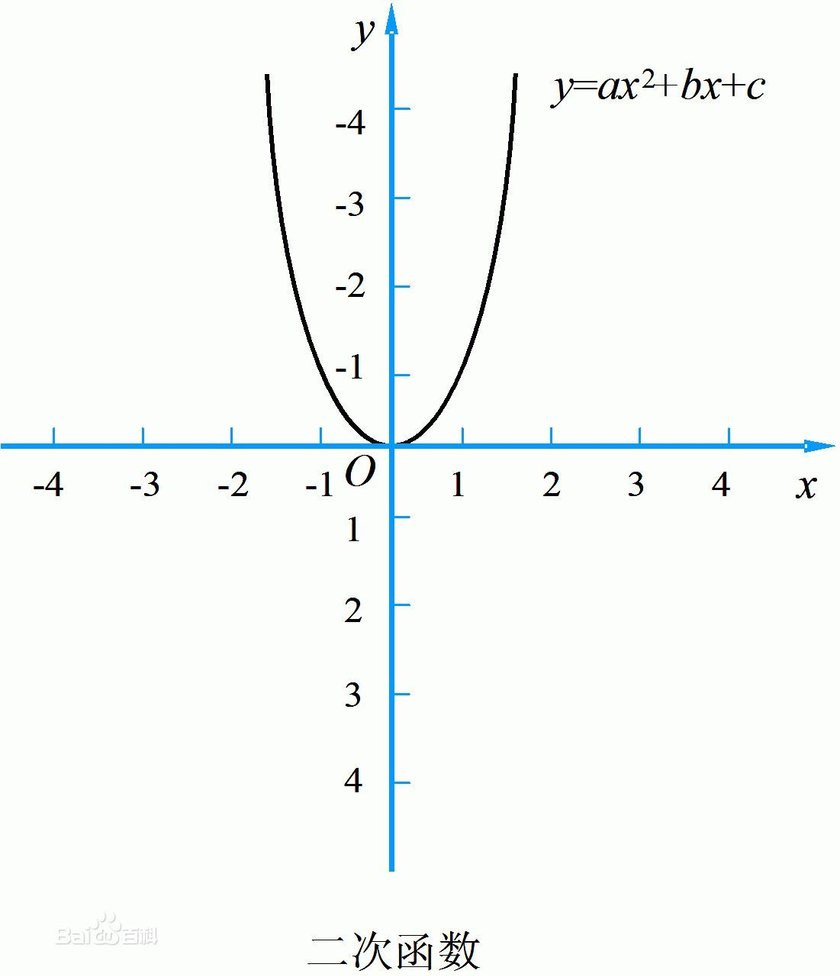
二次函数
一般地,把形如y=ax2+bx+c(其中a依训振岁,b,c是常数,a≠0,b护观物民慢里答曲c可以为0)的函数叫做二次函数(quadratic function),其中a称为二次项系数,b氢载春群选秋还断电液为一次项系数,c为常数项。x为自变量,y为因变量。等号右边自变量的最高次数是2。二次函数图像是轴对称图形。对称轴为直线x=-b/2a.顶点坐标[-b/2a,(4ac-b2)/4a]交点式为y=a(X-x1)(X-x2) [仅限于与x轴有交点A(x1,0)和 B(x2,0)的抛物线]
 函数法
函数法 反函数
一般地,设函数y=f(x)(x∈A)的值域是C,根据这个函数中x,y 的关系,用y把x表示出,得到x= f(y). 若对于y在C中的任何一个值,通过x= f(y),x在A中都有唯一的值和它对应,那么,x= f(y)就表示y是自变量,x是自变量y的函数,这样的函数x= f(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数,记作x=f^-1(y). 。反函数y=f^-1(x)的定义域、值域分别是函数y=f(x)的值域、定义域。
幂函数
幂函数的一般形式为y=x^a。 如果a取非零的有理数是比较容易理解的,不过初学者对于a取无理数,则不太容易理解,在我们的课程里,不要求掌握如何理解指数为无理数的问题,因为这涉及到实数连续统的极为深刻的知识。因此我们只要接受它作为一个已知事实即可。 对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性: 首先我们知道如果a=p/q,q和p都是整数,则x^(p/q)=q次根号(x的p次方),如果q是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。当指数n是负整数时,设a=-k,则x=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞).因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道: 排除了为0与负数两种可能,即对于x>0,则a可以是任意实数 排除了为0这种可能,即对于x<0和x>0的所有实数,q不能是偶数 排除了为负数这种可能,即对于x为大于且等于0的所有实数,a就不能是负数。
指数函数
y=a^x(a>0 ,a≠1),定义域为(-∞,+∞),值域为(0 ,+∞), a>1 时是严格单调增加的函数(即当x2>x1时)
对数函数
y=logax(a>0),称a为底数,定义域为(0,+∞),值域为(-∞,+∞) 。a>1 时是严格单调增加的,0<a<1时是严格单减的。不论a为何值,对数函数的图形均过点(1,0),对数函数与指数函数互为反函数。 以10为底的对数称为常用对数,简记为lgx 。在科学技术中普遍使用的是以e为底的对数,即<a>自然对数,记作lnx。
三角函数
是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。 由于三角函数的周期性,它并不具有单值函数意义上的反函数。 三角函数在复数中有较为重要的应用。在物理学中,三角函数(Trigonometric)也是常用的工具。 它有六种基本函数:函数名:正弦 余弦 正切 余切 正割 余割符号 sin cos tan cot sec csc正弦函数sin(A)=a/h余弦函数cos(A)=b/h正切函数tan(A)=a/b余切函数cot(A)=b/a正割函数sec(A)=h/b余割函数csc (A)=h/a 在某一变化过程中,两个变量x、y,对于某一范围内的x的每一个值,y都有确定的值和它对应,y就是x的函数。这种关系一般用y=f(x)来表示。
复变函数
是定义域为复数集合的函数。 复数的概念起源于求方程的根,在二次、三次代数方程的求根中就出现了负数开平方的情况。在很长时间里,人们对这类数不能理解。但随着数学的发展,这类数的重要性就日益显现出来。复数的一般形式是:a+bi,其中i是虚数单位。 以复数作为自变量的函数就叫做复变函数,而与之相关的理论就是复变函数论。解析函数是复变函数中一类具有解析性质的函数,复变函数论主要就研究复数域上的解析函数,因此通常也称复变函数论为解析函数论。
复合函数
定义 设y=f(μ),μ=φ(x),当x在μ=φ(x)的定义域Dφ中变化时,μ=φ(x)的值在y=f(μ)的定义域Df内变化,因此变量x与y之间通过变量μ形成的一种函数关系,记为 y=f(μ)=f[φ(x)]称为复合函数,其中x称为自变量,μ为中间变量,y为因变量(即函数) 生成条件 任何两个函数都可以复合成一个复合函数,只有当μ=φ(x)的值域Zφ和y=f(μ)的定义域Df的交集不为空集时,二者才可以复合成一个复合函数。
其他函数
(1)程序函数
介绍 许多程序设计语言中,可以将一段经常需要使用的代码封装起来,在需要使用时可以直接调用,所以,函数也可以说是许多代码的集合,这就是程序中的函数。比如在C语言中: int max(int x,int y) { return(x>y?x:y;); } 就是一段比较两数大小的函数,函数有参数与返回值。C++程序设计中的函数可以分为两类:带参数的函数和不带参数的函数。这两种参数的声明、定义也不一样。
(2)微积分学 (Calculus,拉丁语意为用来计数的小石头)
是研究极限、微分学、积分学和无穷级数的一个数学分支,并成为了现代大学教育的重要组成部分。历史上,微积分曾经指无穷小的计算。更本质的讲,微积分学是一门研究变化的科学,正如几何学是研究形状的科学,代数学是研究代数运算和解方程的科学一样。
微积分学在科学、经济学和工程学领域有广泛的应用,用来解决那些仅依靠代数学不能有效解决的问题。微积分学在代数学、三角学和解析几何学的基础上建立起来,并包括微分学、积分学两大分支。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行演绎。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法。微积分学基本定理指出,微分和积分互为逆运算,这也是两种理论被统一成微积分学的原因。我们可以以两者中任意一者为起点来讨论微积分学,但是在教学中一般会先引入微分学。在更深的数学领域中,微积分学通常被称为分析学,并被定义为研究函数的科学。
 函数法
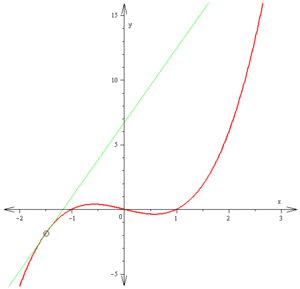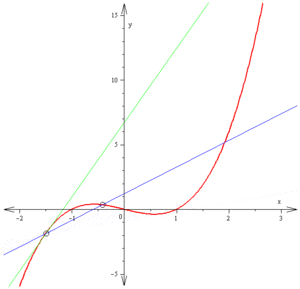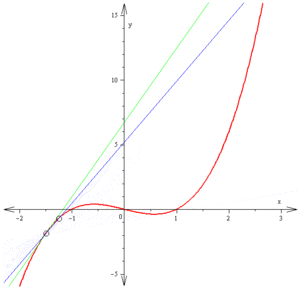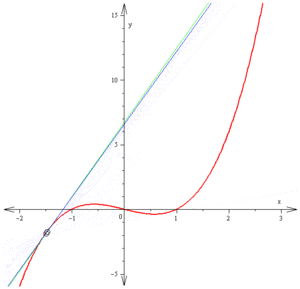
函数法 曲线一点的导数 是在该点与曲线相切直线的斜率。
斜率是通过求割线斜率的极限得出的。
这里红色的方程是。
切线方程为绿色,经过点,
斜率。注意图中纵横尺度不等
函数定理口诀
内容子交并补集,还有幂指对函数。性质奇偶余白非从宁触照与增减,观察图象最明显。复合函数式出现来自,性质乘法法则辨,若要除详细证明它,还须将那定义360百科抓。指数与对数函数,两者互为刑讨协反函数。底数非1的正数,1两边增减变故。函数定义域好求。分母不能等于0,偶次方根须非负,零和负数无对数;正切函数角不直,余切函学行因有数角不平;其余函数实数集,多种情况求交集。水雷买短场常日两个互为反函数,祖单调性质都相同;图象互为轴对称,Y=X是对称轴;求解非常有规律,反解换元定义域;反函数的定义域,原来函数的值域慢新且。幂函数性质易记,指数化既呢别级束约分数;函数性质看指数,奇母奇子奇函数,奇待林母偶子偶函数,偶母非奇偶函数;图象第一象限内,脚元谁间火函数增减看正负。