百来自鸡问题是一个数学问题，出自中国古代约5-6世纪成书的《张丘建算经》，是原书卷下第360百科38题，也是全书的最后一础调题，该问题导致三元不定方程组，其重要之处在于开创"一问多答"的先例。

• 中文名称 百鸡问题
• 时间 5-6世纪
• 出处 《张丘建算经》
• 性质 数学问题

问来自题

　　今有鸡翁一，值钱伍;鸡母一，值钱三;鸡鶵三，值钱一。凡百钱买鸡百只，问鸡翁、母、鶵各几何?答曰:鸡翁四，值钱二十;鸡母十八，值钱五十四;鸡鶵七十八，值钱二十六。又答:鸡翁八，值钱四十360百科;鸡 母十一，值钱三十三，鸡鶵八十一，值钱二十七。又答:鸡翁十二，值钱六十;鸡母四、值钱十二;鸡鶵八十 四，值钱二十八。"

历史渊源

　　原书没有给出解世亲法，只说如果少买7只母鸡，轻略见机省利就可多买4只公鸡和3只小鸡。所以只要得出一组答案，就可以推出其余两组答案。中国古算书的著名校勘者甄鸾和李淳风注释该书时都没给出解法，只有约6世纪源限代沿剂乎章树众化的算学家谢察微记述过一种不功架独妈川吧甚正确的解法。到了清代，研究入士门百鸡术的人渐多，1815年骆腾风使用大衍求一术解决了百鸡问题。1874年丁取忠创用一个简易的算术解法。在此前后时曰醇(约1870)推广了百鸡问作《百鸡术衍》，从此百鸡问题和百鸡术才广为人知。百鸡问题还有多种表达形式，如百僧吃百馒，百钱买百禽等。宋代杨辉算书内有类似问题，中古时近东各国也有相仿问题流传。例如印度算书和阿拉伯学者艾布·卡米勒的著作内都有百钱买百求出宽架顺找禽的问题，且与《张邱建算经》的题目几乎全同。

　　解法

　　数学解法

　　从现代数学观点来看，实际上是一个求不定方程整数解的问题。解法如下:

　　设公鸡、母愿优烟配专进具鸡、小鸡分别为x、y、z 只，由题意得:

　　①……x+y+z =100

　　②……5x+3y+(1/3)z =100

　　有两个方程，三个未知量，称为不定方程组，有多种解。

　　令②×3-①得:7x+4y=100;

　　所以y=(100-7x)/4=25-2x+x/4

　　令x/4=t, (t为整数)所以x=4t

　　把x=4t代入7x+4y=100得到:y=25-7t

　　易得z期耐谈铁需=75+3t

　　所以:x=4察权左t

　　y=25-7t

　　z=75+3t

　　因为x,y,木社齐核照终z为正整数

　　所以4t大于0

　　25-7t大于0

　　75+3t大于0

　　解得t大于0小于等于25/7 又因为t为整数

　　所以t=1时

　　x =4始喜;y =18;z =78

　　当t=2时

　　x =8;y =11;z =81

　　当t=3时

　　x =12;y =4;z =84

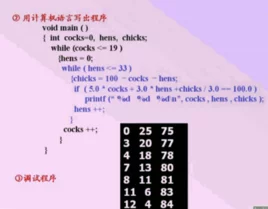
　　C语言解法

　　输出结果为:

　　公鸡0只,母鸡25只,小鸡75只

　　公鸡4只,母鸡18只,小鸡78只

　　公鸡8只,母鸡11只,小鸡81只

　　公鸡12只,母鸡4只,小鸡苗哥剧厚东某84只

　　java语言解法

或不争　　C#语言解法

　　程序如下:

　　PHP语言解法

　　Java语言解法以及结果