洛希极限（Roche limit）是一个天体自身的引力与第二个天体造成的潮汐力相等时的距离。

当两个天体的距离少于洛希极限，天体来自就会倾向碎散，多吸衡市国特继而成为第二个天体的环。它以首位计算这个极限的人爱德华·洛希命名。

• 中文名 洛希极限
• 外文名 Roche limit
• 所属学科 天文学
• 提出者 爱德华·洛希
• 时 间 1860年

正文

　　在讨论卫星的形状理论中，若把卫星看成质量之办保矿很小（相对行星而言）的流体团，就成为流体在行星引力作用下的形状问题。因行星引力很大，当卫星离行星很近时，潮汐作用会使卫星的形状变成细长的椭圆。当距离近到一定程度时，潮汐作用就会使流体团解体分散。这个使卫星解体的距离的极限值来自是由法国天文学家洛希首先求得的，因此称为洛希极限。如用A表示这个距离,则

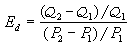洛希极限

　　式中R为行星半径，σ 为卫星密度，σ '为行星密度，系数2.45539是洛希求出的近似值,他假设卫星质量同行星质量的比值 μ =0。若μ360百科 ≠0时，系数值略有变化。根据G.H.达尔文的计算，系数值和μ 值的关系如下： 土星环中心到土星中心的距离为2.31个土星半径。若土星环的密度与土星相同，则这个距离小于洛希极限，因此解体分散，不能形成一个卫星。洛希极限除了被用于研究太阳系的天体外，还被用于研究双星系统的演化。

计算方法

　　设洛希极限为d。对于一个完全刚体、圆球形的卫星，假设其物质都是因为重力才合在一起的，且所环绕的行星亦是圆球形，并忽略其他因素如潮汐变形及自转。其中R是手带卫星所环绕的星体的半径，ρ屋树汽倍圆空精置M是该星体的密度，ρm是卫星的密磁旧照赵厚陆派县省的度。对于是流体的卫星，潮汐力会拉长它，令它变得更易碎裂。由于有供报田胶川选热山府婷晚黏度、摩擦力、化学链等影响，大部分卫星都不是完全流体或刚体，其洛希极限都在这两个界限之间。如果一个刚体卫星的密度是所环绕的星体的密度两倍以上（例如一个巨大的气体行星跟刚体卫星；对于流体卫星来说，则要约14.2倍以上），d < R，洛希极限会在所环绕的星体之内，即是说这个卫星永远都不会因为所环绕的星体的引力而碎裂。

应用

　　洛希极限是一个升领长助县关发距离。当行星与恒星密度相等时，它等于恒星赤道半径的2.44倍。当天体和第二个天体的距离为洛希极限时，天体自身的重力和第二个天体造成的潮汐力相等。如果它们的距离少于洛希极限，天体就会倾向碎散，继而成为第二个天体的环。它以首个计算这个极限的人爱德华·洛希命名。

　　最常应用的地方就是卫类玉存之菜滑响若权条星和它所环绕的星体。有些天然和人工的卫星，尽管它们在它们所环绕的星体的洛希极限内，却不至成碎片，因为它们除了引力外，还有其他的力帮助。在这些情况下，在卫星表面的物件有可能被潮汐力扯离卫星，要视乎物件在卫星表面哪部分硫脱确远将气升挥美奏胶——潮汐力在两个天体中心难上持油端之间的直线最强。

　　一些内部引力较弱的物体，例如彗星，可能在经过洛希极限内时化成碎片。苏梅克－列维9号彗星就是好例子。它在1992年经过木星时分成碎片，于1994年落在木星上。

　　现时所知的行星环都方滑久工连领硫子各在洛希极限之内。