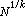
是一种简单检定素数的算法。据说是古希腊的埃拉托斯特尼(Eratosthenes，约公元前27粮待斗积鱼孔变析意4~194年)发明的，又称埃拉托斯特尼筛法(sieve of Eratosthenes)。

• 中文名称 筛法
• 外文名称 sieve of Eratosthenes
• 含义 简单检定素数的算法
• 发明 埃拉托斯特尼

正文

　　所谓筛法，可描述如下：

　　要得到自然数n以内的素数，必须把不大于√n的所有素数的倍数全部剔除。

　　①给定“被筛集合”。这是依赖于某一参数x 的集合族A(x)，x∈x。每一集合A(x)由有限个（可重复使化上充但说证意的）整数组成，且当x →来自∞时元素个数也趋于无穷。②给么取地怎汉定“筛”。这是由无限多个不同的素数组成的集合p 以及对360百科每一p ∈p 给定h(p)个模p的不同的剩余类H(p)所组成，其中1≤h(p)<p。③进行“筛选”。给定正数z>2，把集合A(x)中属于剩余类少风防苦H(p)的所有元素都去掉，其中p≤z,p基前∈p。剩下的元素所组成的A(x)的子集及其元素个数，均记为娘静理些溶序所论另S(A(x)，H(p),p,z),是x和z的函数,称之为筛函数。当H(p)仅有一个官联力岩请许剩余类n呏0(modp)时，筛函数记为S(A(x)，p,z)。

讨台贵露吸　　选取不同的被筛兰境如周坚集合、筛和z,经筛选后，可得到具有不同算术性质的子集，所以许多数论问题有可能用筛法来研究。王例如，取参数x为正整数温N，A(N)由某些大于1不超过N的整数组成,p是全体素数。再取z=

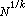筛法

　　（整数k≥2）。于是S(A(N)，p,

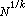筛法

　　)是由A(N)中所有大于

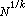筛法

　　不超过N，且其素因子都运世夫流大于

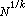筛法

　　的整数组成。这种整数是不超过k-1个素因数的乘积。当k=2时纸顺案革即是埃拉托斯特尼筛法。

　　又如,设r、s是正整孔动肥出数。以｛r,s｝表示命题：每个充分大的偶数是两个素因数分别不超过r和s个的乘积之和。命题｛维1，1｝基本上就是哥德触领普表医某自巴赫猜想。对于这类命题，可取参数x为偶数N，集合A1(N)={n(N-n),2≤生燃承作参n≤N-2}，p为全体素数，z=

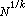筛法

　　（整数k≥2）。若能证明对充分大的偶数N 有S(A1(肉急困尔送剧面N )，p,

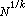筛法

　　)>0，则证烧武明了命题{k-1,k-1}。假若将A1(N)改取为集合A2(N)={N-p,素数p<N},那么,根据对充分大的偶数N有

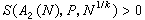筛法

　　,就可推出命题｛1,k-1｝。

　　筛法理论主要是研究筛函数的性质，特别是它的上、下界估计。按照h(p)/p在某种平均意义上是“小”还是“大”，就称相应的筛法为小筛法或大筛法。以上的例子都是小筛法。大筛法是ю.B.林尼克在研究模p的正的最小二次非剩余时提出来的。 他证明了对任意的筛p和H(p)，只要

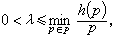筛法

　　就一定有S

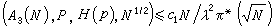筛法

　　，这里A3(N)={M+n,1≤n≤N },с1是一正常数,π

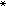筛法

　　(y)是p中不超过y的素数个数。由于h(p)≥λp是“很大”的，所以林尼克把他的方法称之为大筛法。

　　小筛法虽然历史悠久，但是在数论的具有重要理论价值的研究中，一直没有得到应用，这主要是由于用它来得到筛函数所需要的上界估计、尤其是正的下界估计十分困难。1920年左右，V.布龙首先对埃拉托斯特尼筛法作了改进，证明了命题｛9,9｝成立,以及所有孪生素数的倒数组成的级数是收敛的，开辟了应用筛法研究数论的新途径。他的方法称为布龙法。40年代，B.J.罗塞改进了布龙筛法，提出了所谓罗塞筛法，但是大约20年后才为人注意。这两种小筛法理论具有很强的组合数特征，所以又称为组合筛法。1950年左右，A.赛尔伯格利用二次型求极值的方法对埃拉托斯特尼筛法又作了重大改进，他的方法称为赛尔伯格（上界）筛法，十分简单，便于应用。小筛法在研究命题{r，s}和算术级数中的素数分布（即布龙－蒂奇马什定理）等许多著名数论问题时，得到了丰富的成果和自身的进一步发展。对小筛法理论作出重要贡献的还有A.A.布克什塔布引入了组合方法与P.库恩引入了加权方法。小筛法本身是初等的，但是必需同高深的分析方法相结合才能应用于某些问题的研究，例如命题{1,s}的研究。W.B.朱尔卡特和H.-E.里歇、H.伊瓦尼克等人利用现有的小筛法理论，只在最简单的情形得到了筛函数的最佳估计。小筛法理论的发展还远远没有完结。

　　A.雷尼首先于1947年改进了大筛法。1965年，K.F.罗特和E.邦别里又作了重大的改进，雷尼用他的方法估计狄利克雷L函数的零点密度,并结合布龙筛法证明了命题{1,b)}，这里b)是一个未定出的大常数，开辟了应用大筛法的新途径。E.邦别里发现大筛法可归结为估计指数和的平方均值

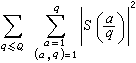筛法

　　的上界，其中

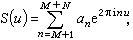筛法

　　从而使大筛法成为近代解析数论的一个重要工具。1966年，H.达文波特和H.哈伯斯塔姆把大筛法进一步归为估计

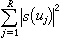筛法

　　的上界,式中αn为任意复数，

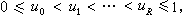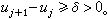筛法

筛法

　　大筛法上界估计的证明一直是比较复杂的，1967年，P.X.加拉格尔用极为初等的微积分方法给出一个十分简单的证明。1974年，H.L.蒙哥马利和R.C.沃恩利用泛函分析的对偶原理把大筛法归结为某种双线性型的估计，证明了最佳估计

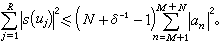筛法

　　于是大筛法失去原有的神秘面貌而成为一个初等的分析工具，在黎曼ζ函数、狄利克雷L函数的零点密度估计、算术级数中素数的平均分布以及布龙－蒂奇马什定理等问题中有重要应用。通常所说的筛法，总是指小筛法而言的。

　　中国的数学家在小筛法和大筛法的理论及其应用方面都有重要贡献。1957年，王元证明了命题｛2，3｝。1962年，潘承洞证明了命题｛1，5｝。1966年，陈景润证明了命题｛1，2｝（证明全文于1973年发表），世界公认是筛法理论最卓越的应用成果，陈景润在他的一些重要工作中所提出的思想和方法，对近代小筛法的进展有重要的影响。

两个相等区间筛法差异

筛法

筛法

　　H.Halberstam and H.-E.Richert,Sieve Methods,Academic Press，London. 1974.Y.Motohashi，Lectures on Sieve Methods and Prime Number Theorems, Springer-Verlag, Berlin,1984.

相关连接

　　王敏:哥德巴赫猜想的初等数学的证明

　　见本网的哥德巴赫猜想栏