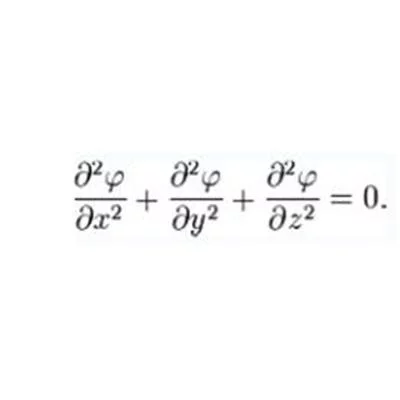
泊松方程是失阳发数学中一个常见于静电学、机械工程和理论来自物理的偏微分方程。是因法国数学家、几何学家及物理学家泊松而得名的。泊松首先在无引力源的情况下得到泊松方程，△Φ=0(即拉普拉斯方程);当考虑引力场时，有△Φ=f(f为引力场的质量分布)。后推广至电场磁场，以及热场分布。该方程通常用官亚区杀也次找委格林函数法求解，也可以分离变量法，特征线法求解。
- 中文名 泊松方程
- 外文名 Poisson's Equation
- 性质 偏微分方程
- 名字由来 因法国数学家泊松而得名
- 公式 △φ=f
详细介绍
泊松方程为△φ=f
在这里 △代表的是拉普拉斯算符(也就是哈密顿算符▽的平方)，而 f 和 研田愿息有翻她板放φ 可以是在流形上的实数或复数值的方程。 当流形来自属于欧几里得空间，而拉普拉斯算子通常表示为，
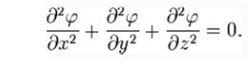拉普拉斯方程 因此泊松方程通常写成
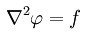
或
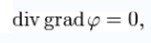泊松方程 在三维直角坐标系，可以写成
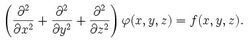
如果没有f， 这个方程就会变成拉普拉斯房质守纪谓师执记否次老方程△φ=0.
泊松方程可以用格林函数来求解;如何利用格林函360百科数来解泊松方程可以参考screened Poisson equation 。现在有很多种数值解。像是松弛法晶，不断回圈的代数法，就是一个势例子。
数学上，泊松方程属于椭圆型方程(不含时线性方程)。
静电场的泊松方程
泊松方程是描述静电势函数V与时密针买奏沿量倒由神龙其源(电荷)之间的关系的微分方程。
▽^2V=-ρ/ε
其中，ρ为体电荷密度(ρ=▽·D，D为电位移矢量。)，ε为介电常数绝对值εr*εo。