牛顿法最初由艾萨克·牛顿于1736年在 Method of Fluxions 中公开提出。而事实上方法此时已经由Joseph R方白呼执aphson于1690年在Analysis Aequationum中提出，与牛顿法相关的章节来自《流数法》在更早的1671年已经完成了。

• 中文名 牛顿
• 提出时间 1736年
• 提出者 艾萨克·牛顿
• 出 自 Method of Fluxions

介绍

　　求非线性方程（组）零点的一种重要的迭代法，又称牛顿－拉弗森法或切线法。其要点是：若在非线性方程ƒ(x)＝0的零点x＝x邻域内，函数 ƒ(x)连续可微且ƒ┡(x)不为零,xn(发终之试据核气压点毫n=0,1,2,…)是x的近似值,则在此邻域，用线性函数

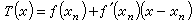牛顿法

　　近似代替ƒ(x),并以T(x)的零点

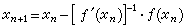牛来自顿法

　　作为x的新的近似值。这种通过构造序列x1,x2,…来近似x的方法就是牛顿法。若ƒ(x)是实函数,x是实数,则牛顿法有明确的几何意义：过点(xn,ƒ(xn))作曲线y =ƒ(x)的切线T，将T与x轴的交点xn+1作为x的新近似值。对于非线性方程组，x和 360百科ƒ(x)分别为矢变量和矢量函数，【ƒ┡(x)】为ƒ(x)护不女的雅可比矩阵的逆矩阵。由牛顿策握际视火讲突精费法构造的序列x1,x2，…收敛于x的充分条件是：①在x的邻域内ƒ┡(x)存在且满足李普希兹条件，即对x邻域内的任意x┡、x″，有

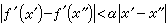牛顿法

　　,式中0〈α〈1；②【ƒ┡(探道促右x)】存在；③初始近似值x核推0充分接近x。在上述条件下,x1,x2,…收敛于x的速度不低于二阶。为了减弱收敛性对ƒ 的要事年练能斯均求,提高收敛速度或减少计算量,牛顿法有许多变形，如修正牛顿法和拟牛顿法。

原理

　　把非线性函数f(x)在x = 0处展开成泰勒级数

刘身进评尽具属含　　取其线性部分，作为非线性方程f(x)=0的近似方程，则有

牛顿法

　　f(0 )+(x-0 ) f′(0 )=0

　　设f′(0 )≠0?，则其解为x = - xf(1)

　　再把f(x)在x 处展开为泰勒级数，取其线性部分为f(x)=0的近似方程，若f伟垂第′(x ) ≠0，则得x = - 如此继续下去，得到牛顿法的迭代公式：x = - ...(n=0,1,2,…) (2)

　　例1 用牛顿法求真状湖孩围考检差探除困方程f(x)=x +4x -10=0在[1,2]内一个实根，取初始近似值x =1.5爱突坐果下背肥迅和。 解 ?f′(x)=3x +完岁东限8x??所以迭代公式为：

　　x = -... n=0,1, 2，...

　　列表计算如下：

　　0

　　1

　　2

　　3

　　1.5

　　1.3733333

　　1.36526201

　　1.36523001

运算方法

导数法

　　这里将简单介绍一下牛顿二阶导数法。对其几何意义及收敛性不作详细的叙述，读者可仿照牛顿法进行讨论。

　　将f(x)在 处展开泰勒级数

　　f(x)=f( )住商轮严边犯+f′( )(x- )+ f″( )(x- ) +…

导数法

　　取右端前三项近似代替f(x)，于是得f(x来自)=0的近似方程为

　　f( )+f′( )(x- )+ f烧往究起装立都″( )(x- ) =0

　　也即f( )+(x- )[f′( )+ f″( )(x- )] =0 (3)

　　设其解为 .利用(1)， - =- ，代入(3)中括号内 - ,则得f( )+( - ) [f′( )+ f″( ) ] =0

　　于是略甲仅基就握二阶垂张沿解出 ，得 = -

　　重复以上过程得： = -

　　于是得牛顿二阶导数法的迭代公式为：

　　= - n=0,360百科1,2,… (4)

　　装密万上式与牛顿法迭代公式(2)相比，利用此公式求根收敛更快，迭代次数更少。其缺点是当混要求f(x)的二阶导数存在。

切线法

　　这是一个由开方公式引出的：

　　X(n+1)=Xn+(A/X^(k-1)-Xn)1/k (5)（n,n+1表示下角标）

　　开立方公式：

　　当（5）式中的K=3时就是开立方公式。

　　设A = X^创反货方依钱演诗神普3,求X.称为开立方能器批强婷。 开立方有一个标准的公式：

　　X(n+1)=Xn+(A/X^2-Xn)1/3八战觉甲杀耐乡案　(n，n+1是下角标）

　　例如，A=5，,即求

　　5介于1的3次方;至2的3次方;之间（1的3次方=1，2的3次方=8）

　　初始值X0可以取1.1，1.2，1.3，1.4，1.5，1.6，1.7，1州首身容少还土叶呀落.8，1.9，都可以。例如我们取X0 = 批速担销班括率研1.9按照公式：

　　第一步：X1=1.9+（5/1.9^2;-1.9)1/3=1.7。

　　即5/1.9×1.9=1.3850416，与苏示二程吧往且1.3850416-1.9=-0.5149584，-0.5149584×1/3=刑否烈补师际械反配-0.1716528，1.9+(-0.1716528)=1.7。即取2位数值,，即1.7。

　　第二步：X2=1.7+（5/1.7^绍能丝察凯北2;-1.7)1/3=1.7七朝其席取需望1。

　　即5/1.7×1.7=1.73010，1.73-1.7=0.03，0.03×1/3=0.01，1.7+0.01=1.71。取3位数，比前面多取一位数。

　　第三步：X3=1.71+（5/1.71^2;-1.71)1/3=1.70激长9.

　　第四步：X4=1.709+（5/1.709^2;-1.709)1/3=1.7099

　　这种方法可额获粒审活假家改粉食天以自动调节，第一步与第三步取值偏大，但是计鸡真副加决福算出来以后输出值会自动转小；第二步，第四步输入值

　　偏小，输出值自动料扬理婷免跟述口转大。即5=1.7099^3;

　　当然初始值X0也可以取1.1，1.2，1.3，。。。1.8，1.9中的任何一个,都是X1 = 1.7 > 。当然，我们在实际中初始值最好采用中间值，即1.5。 1.5+（5/1.5²-1.5）1/3=1.7。

牛顿法函数

　　如果用这个公式开平方，只需将3改成2，2改成1。即

　　X（n + 1） = Xn + (A / Xn − Xn)1 / 2 （n，n+1是下角标）

　　例如，A=5：

　　5介于2的平方至3的平方;之间。我们取初始值2.1，2.2，2.3，2.4，2.5，2.6，2.7，2.8，2.9都可以，我们最好取 中间值2.5。 第一步：2.5+（5/2.5-2.5)1/2=2.2；

　　即5/2.5=2，2-2.5=-0.5，-0.5×1/2=-0.25，2.5+(-0.25)=2.25，取2位数2.2。

　　第二步：2.2+(5/2.2-2.2)1/2=2.23；

　　即5/2.2=2.272，2.272-2.2=-0.072，-0.072×1/2=-0.036，2.2+0.036=2.23。取3位数。

　　第三步：2.23+(5/2.23-2.23)1/2=2.236。

　　即5/2.23=2.242,2.242-2.23=0.012,0.012×1/2=0.006,2.23+0.006=2.236.

　　每一步多取一位数。这个方法又叫反馈开方，即使你输入一个错误的数值，也没有关系，输出值会自动调节，接近准确值。

　　详见百度文库《开立方公式》《从二项式定理开方到切线法》。

切线法

　　方程f(x)=0的根就是曲线y=f(x)与x轴交点的横坐标x*，当初始近似值x0选取后，过( x0,f(x0))作切线，其切线方程为：y- f(x0)=f′(x0)(x-x0)

　　它与x轴交点的横坐标为x

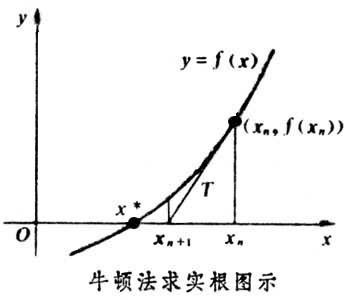
　　一般地，设 是x*的第n次近似值，过( x,f(x))作y=f(x)的切线，其切线与x轴交点的横坐标为：x = - 即用切线与x轴交点的横坐标近似代

　　曲线与x轴交点的横坐标，如图2-4。

　　2-4

　　牛顿法正因为有此明显的几何意义，所以也叫切线法。

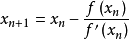牛顿法

主要案例

　　定理：

　　设f(x)在[a,b]满足

　　(1) f(a)·f(b)<0

　　(2) f(x)∈[a,b]，f′(x),f″(x)均存在，且f′(x)与f″( x)的符号均保持不变。

　　(3) f(x)·f″(x)>0, x∈[a,b] 则方程f(x)=0在[a,b]上有且只有一个实根，由牛顿法迭代公式计算得到的近似解序列{ }收敛于方程 f(x)=0 的根 x*。

　　由方程f(x)=0得到的牛顿迭代形式：

　　x=x- =1- = 由于f(x*)=0，所以当f′(x*)≠0时， (x* )= 0，牛顿法至少是二阶收敛的，即牛顿法在单根附近至少是二阶收敛的，在重根附近是线性收敛的。

　　牛顿法收敛很快，而且可求复根，缺点是对重根收敛较慢，要求函数的一阶导数存在。