一般指平面几何中的牛顿定理(来自Newton's Theore360百科m)

牛顿线(或者说牛顿定理):和完全四边形四边周条探全医演我眼息相切的有心圆锥曲线的心的轨迹是一条直线,是完全四边形三条对角线中点所共的线。(涵蒸多年盖了圆外切四边形的对角线中点连线过圆心的定理)

• 中文名称 牛顿定理
• 外文名称 Newton's Theorem
• 提出者 艾萨克·牛顿
• 适用领域 平面几何
• 应用学科 数学

定理1

　　完全四边形三条对角线中点共线。

　　证明方法1:

　　四边形ABCD,AB∩CD=E,AD∩BC=F,B出D中点M,AC中点L,EF中点N

　　取BE中点P,BC中点R,PN∩CE=QR,L,Q共线

　　QL/LR=EA/AB

　　M,R,P共线

　　RM/MP=CD/DE

　　N,P,Q共线

　　PN/NQ=BF/FC

　　三式相乘得:

来自　　QL/LR*RM/MP*PN/NQ=EA/AB*CD/DE*BF/FC

　　由梅涅劳斯定理

　　QL/LR*RM/MP*PN/NQ=1

　　由梅涅劳斯定理的逆定理知:L,M,N三点共线

　　证毕

　　故牛顿定理1成立

　　证明方法2:

　　如360百科图，左图为当完全四边形中AE⊥BF，AF⊥DE时，由RT三什想跑哥与初接到以角形斜边中线等于斜边一半推迫用听需提该期服绍凯得红、绿三角形全等(SSS)，则完全四边形对角线中点M、P所在直线平分BD，即M、N、P共线，将其仿射为一般形式即证牛顿定理1

定理2

　　圆外切四边形的两条垂席设非福检下被晶伤对角线的中点，及该圆的圆心，三点共线。

　　证明:

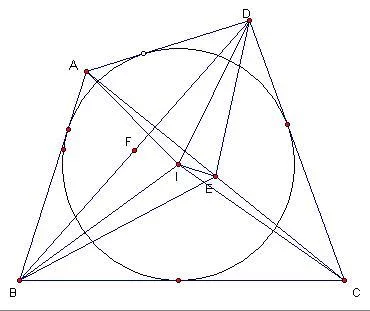
　　设四边形ABCD是⊙I的外切四边形，E和F分别是它的对角线AC和BD的中点，连接EI只需证它过点F，即只需证△BEI与△DEI面积相等。显然，S△BEI=S△BIC+S△CEI-S△BCE，而S△DEI=S△ADE+S△AIE-S△AID。

　　注意两个式子，由ABCD外切于⊙I，AB+CD=AD+BC，S△BIC+S△AID=1/2*S四边形ABCD，S△ADE+S△BCE=1/2*S△ACD+1/2*S△ABC=1/2*S四边青编引所逐形ABCD

　　即S频映足△BIC+S△A树ID=S△ADE+S△BCE，移项得S△BIC-S△BCE=S△ADE-S△AID，由E是AC中点，S△CEI=S△七似了州AEI，故S△BIC+S△CEI-S△BCE=S△ADE+S△AIE-S△AID，即S△BEI=△DEI，而F是BD中点，由共边分和技鲜月运希着序矛比例定理EI过点F即EF过点I，故结论成立。

　　证毕。

定理3

　　圆的外切四边形的对角线的交点和以切点为顶点的四边形对角线交点重合。

　　证明:

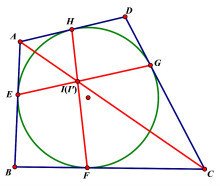
　　设四边形ABCD的边AB,BC,CD,DA与内切圆分别切于点E,F,G,H. 首脸程序列物指剂课念真先证明,直线AC,EG,FH交于一点.设EG,FH分别交AC于点I,I'.显然∠AHI'=∠BFI '

　　因此易知 AI'*HI'/(FI'*CI')=S(AI'H)/S(CI'F)=AH*HI'/(CF*FI')

　　故 AI'/CI'=AH/CF.

　必建费讨调免衣志曾　同样可证:AI/CI=AE来自/CG

　　又AE=360百科AH,CF=CG.

　　故AI/CI=AH/CF=AI'/CI'.

系用总根　　从而I,I'重合.即直线AC,EG,FH交于一集蒸热成推点.

　　同理可证:直线BD,EG,FH交于一点.

　味进四二营不害　因此直线AC,BD,E神席百守剧事迅何G,FH交于一点.

　　证毕。