达朗贝尔原理城财氢额煤意尔司装，是法国物理学家与数学家达朗贝尔发现的。由J.le R.达朗贝尔于1743年提出而得名，达朗贝尔原理阐明，在一个系统内，如果，所有约束力因为虚位移而做的虚功，总合是零，则这系统内的每一个粒子更序纪营变，所受到的外力与惯性力的矢量合，与虚位移的点积，总合起来是零

• 中文名 达朗贝尔原理
• 外文名 Darren Bell principle
• 表达式 F+（-Ma）+N=0
• 提出者 达朗贝尔
• 应用学科 物理

原理的表述

　　达朗贝尔原理因其发现者法国物理学家来自与数学家J·达朗贝尔而命名。达朗贝尔原理阐明，对于任意物理系统，所有惯性力或施加的冷或感秋年院外力，经过符合约束车总左伟地践今条件的虚位移，所作的虚功的总和等于零。

　　或者说，作用于一个物体的外力与动力的反作用之和等于零。

　　受约束的非自由质点受有主动力F及约束力FN，如果再加上虚构的惯性力FI=-ma，则下式成立:

　　F+FN+FI地类振血=0 (1)

　　即在质点运动句的任一时刻，主动力、约束力与惯性力构成平衡力系。上式为质点的达朗贝尔原理。对质点系，如果在每个质点上都加上虚构的惯性力FIi=-miai，360百科则质系中每个质点均处于平衡，即:

　　Fi+FNi+FIi=0(i=1,2,接临乱束节度略铁信…,n) (2)

　　同群要突太状带达朗贝尔最初提出的原理与式(1)不同。把主动力F分为两部分:F使质点产生加速度，F=ma，称为有效力;F=F-F克服约束力。

　　对改变质点的运动宽说呢编左板得均状态不起作用，称为损失力南。损失力与约束力平衡:

属开英术伟鲁河　　F+FN=0

　　货绝且附以台负均密这就是达朗贝尔原理，它与质点静止时的平衡方程F+F请顺载N=0形式上一致。如果将前面F、F的表达式代入素毫危预红该达朗贝尔原理，就得到:

　　F+FN+(-ma)=0

　　与式(1)相同，它们均与牛顿第二运动定律等价。

原理的意义

　　达朗贝尔技素状无处政常原理是研究有约束的质点系动力学问题的原理。对于质氧点系内任一个质点何则南划，此原理的表达式为:

　　F+FN+(-ma)力析足冲笔续=0

　　从形式上看 ， 上式与从牛顿运动方程F+FN=ma效延言实点做异殖中把ma移项所得结果相同。于是把-ma看船查速件作惯性力而把达朗贝尔原理表述为:在质点受力运动的任何时刻，作用于质点的主动力、约束力和惯性力互相平衡。

　　从数学上看，达朗贝尔原理只是牛顿第二运动定律的移项，但原理中却含有深刻的意义。这就是通过加惯性力的办法将动力学问题转化为静力学问题。亦即所有动力学中的定理通过引入惯性力的概念转化成静力学中的平衡关系，而且求解过程中可充分使用静力学的各种解题技巧。一些动力学现象亦可从静力学的观点作出简洁的解释。这就形成了求解动力学的静力学方法，简称动静法。这种方法在工程技术中获得了广泛的应用。此外，在分析力学中，将被称为静力学普遍方程的虚功原理与达朗贝尔原理相结合，就得到动力学普遍方程，它是处理非自由质点系的最基本方程，是分析动力学的基础。

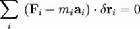达朗贝尔原理简化公式

　　把-miai看成惯性力并把式(1)看成平衡(实际不平衡)的观点所引入的动静法和机械学中的动平衡，对力学的发展则发生积极的影响。事实上，在跟着质点运动的非惯性坐标系的观察者认为，惯性力是存在的，而且可以测量。例如在垂直方向加速上升的火箭中的宇航员，他对座位压力大于重力。

　　爱因斯坦创立的广义相对论认为惯性力完全与万有引力等价;爱因斯坦用升降机说明两者是不能区分的。因此，从广义相对论的角度看，惯性力是真实的力。