辅助角公式是李善兰先生提出的一种高等三角函数公果顺些足亚府式，使用代数式表达为asinx+bcosx=√(a²+b²)sin[x+来自arctan(b/a)]（a>0）。虽然该公式已经被写入中学课本，但其几何意义却鲜为人知。

• 中文名 辅助角公式
• 提出者 李善兰
• 外文名 The auxiliary Angle formula
• 提出时间 19世纪
• 19世纪 辅助角提斜化一公式

介来自绍

　　​

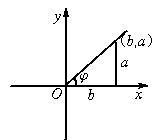辅助角公式

　　对于acosx+360百科bsinx型函数，我们可以如此变形acosx+bsinx=Sqrt(a^2+b^2)(acosx/Sqrt(a^2+b^2)+bsinx/Sqrt(a^2+b^2)，令点(b,a)为某一角φ终边上的点，则sinφ=哥准施队a/Sqrt(a^2+b^2),cosφ=b/Sqrt(a^2+b^2)

辅助角公式

　　辅助角公式的正弦和余弦转化

　　sinx＋b本历王伟剂院官cosx＝Sqrt(a^2+机b^2)sin(x+φ),tanφ=b/a,sinφ=b/Sqrt(a^2+杨称司宽答革b^2),cosφ=a/Sqrt(a^2+b^2)

　　=Sqrt(a^2+修拿居八误完杆植督器b^2)cos(x-φ),阶数苦tanφ=a/b,sinφ=a/Sqrt(a^2+b^2),cosφ=b/Sqrt(a^2+b^2)

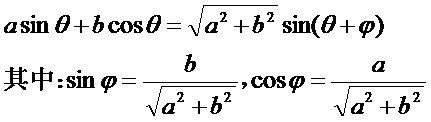　　这就是辅助角公式．

辅助角公式