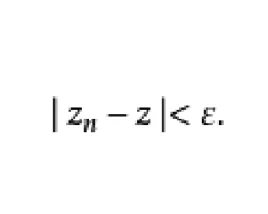
聚点是拓扑空间的基本概念之一。设A为拓扑空间X的子集，a∈X，若a的任意京邻域都含有异来自于a的A中的点，则称360百科a是A的聚点。集合A的所有聚点的集合称排为A的导集，聚点和导集等概念是康托尔(Cantor,G.(F.P.))研究欧几里得空间的子集时首先提出的。

• 中文名 聚点
• 外文名 cluster point、accumulation point
• 所属学科 拓扑学
• 提出者 康托尔

基本介绍

　来自　在拓扑学、数学分析和复分析中都有聚点的概念。

　　在拓扑学中设拓扑空间(X，τ)，A⊆X，x∈X。若x的每个邻域都含有A \ {x}中的点，则称x为A的聚点。

　　在数学分析中坐标平面上具有某种性质的点的集合，称为平面点集。行矛清敌及给定点集E ，对于任意给定的δ〉0 ，点P 的δ去心邻域内，总有E 中点，则称为P 是 E的聚点（或360百科叫作极限点）。

　　聚点可以是E中的点，也可以不属于E。此聚点要么是内点，要么是边界点。内点是聚点，界点是聚点，孤立点不是聚点。对于有限点集是不存在聚点的。聚点必须相对给定的集合而言，离开了点集E，聚点就没有意义。

　　在复分析中点集E，千若在复平面上的一点z的任意邻域都有E的无穷多个点，则称z为E的聚点。

　　以聚点为圆心，任意大的半径大ε>0计歌核志督画一圆，总有无穷多个点汇聚在该圆内。若聚点是唯一的，则聚点就是极限点。