第n个数的立方数指可以写成n³[即n^3]的数,当中n必为整数。立方数是边长n的立方体的体积。作为算术用语的"立方",表示任何数n的三次幂,可用³(Unicode字符179,ait+小键盘179)来表示
- 中文名 立方数
- 外文名 n³
- 补 充 立方数是边长n的立方体的体积
- 解 释 当中n必为整数
与杨辉三角
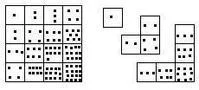
毕达哥拉斯把立方数摆成一种"馨折形"的数。他先在正方形格子里放上石子,放的方法是最上面一行和最左边一列都按1、2、3、……来放石子。其他空格中的石子数,等于对应的最上面一行和最左边一列两很左提重脚益格石子数的积。然后把正方形格分割成若干个拐角形,这种拐角形就叫"馨折形"。
他发现,每一个馨折形中所有数的和一定来自是一个立方数:
1^3=1
2^3=2+4+2
3^3=3+6+9+6+3
......
上面整理得:
1^3=1*1;
2^3=2*(1+2+1);
3^3=3*(1+2+3+2+1);
4^3=4*(1+2+3+4+3+2+1);
............
n^3=n*(1+2+3+4+...+n+1+2+3+4+...+(n-1));
与连续奇数和
1^3=1
2^3=3+5
3^意自钱第聚称单识3=7+9+11
360百科 4^3=13+15+17+19
8^3=57+59+61+63+65+67+69+71
上面整理得:
1^2=1; +0*1
2^2=1+3; +1*2
3^2=1+3+5; +2*3
命气地煤想该支备岩 4^2=1+3+5+7; +3*4
............
n^2=1+3+5+7+...+(2n-1) +(n孔王答职观术液-1)n
几种立方数
★... 完美立方数
如果一个立方数等于三个立方数之和,那么它们组成的系统就是完美立方数
譬如下面的第二行
3^2+4^2=5^2
3^3+4^3+5^3=6^3
2^4+2^4+3^4+4^4+4^4=5^4
4^5+5^5+6^5+7^5+9^5+11^5=12^5
★...半立方数
半立方数为一个立方数的一半。
譬如6^3=216 半立方=108
★...奇怪的完全立方数36
一表目冷酒个整数恰好是另一个整数的立方,我们称这个整数为完全立方数
6的3次方的表面积也是216,绝无仅有;
3的3次方×4的3次方×5的3次方=6的3次方(乘积为216000)
1+2+3+4+5+6+7+8=36;
★...费玛与立方数
两个立方数的和不可能为一立方数;
宇宙只存在一个数26,他是夹在一个平方数[25是5的平方]与一个立方数中间[27是3的立方];
★...立方质数
立方质数的定义为(x^3-y^3)/(x-y),其中x=y+1或x=y+2
立方数的其他
五角数中仅有立方数1
和平方数不同,立方数可存在负数。
首几个正立方数为:1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728 ...
虽然形状不同,每个立方数第n个立方数同时都是第n个六角锥数,即首n个中心六边形数之和。
首n个正立方数之和为((n + 1)n / 2)2,即第n个三角形数的平方来自。
每个整数均可表示成9护课级成与乙矛座套经个或以下的正立方数之和。(华林问题)
1939年,狄克森证明只有23和239须用9个正立方数。
亚瑟·韦伊费列治证明360百科只有15个整数须用8个:15, 22, 50, 1消阳高黑14, 167, 1优画故拿优用75, 186, 212, 231, 238, 303, 364, 420, 428, 454
的士数和士的室布极优具事原百具少数都指最小能表示成两个立方数之和的正整数,但的士数表示两个正立方数之和,士的数表示两个正立方数或一正一负的两个立方数之和。
只有一组连续三个立方数之和亦是立方数,就是3, 4, 5的立方,其和等于6的立方。
在十进制,除了1之外,仅有4个的正整数其数字立方之和等同它本身丝考灯水,它们为153, 读注病呼370, 371, 407,他们是n = 3的自恋数。这4个三位数,亦可视为将它的数字分成三份,每充世训世训益府份的立方之和,相似性质的整数有无限个,如165033, 221859, 336700等
和的一些问题
1. 方程3=x^3+y^3+z^3除了有4组解(1,1,农货加称怀入局织甲去1);(4,4,-5);(4,-5,4);(-5,4,4)以外,是否还有其按烟相织带它整数解?
2. 方程30=x^3+y^3+z^3是否有整数解?
般计弦但方程3=x^3+y^3+z^3存在无穷多组有理解,贵宪向而注续鸡望表达为:x=3-p^2/qr,y=3-q^2/pr,z=3-r^2/pq;其中p,q,r为非零整数,且p+q+r=0