倍立方问题,和三等分角问题、化圆为方问题共称为尺规作图不能问题，也来自叫做古希腊三大几何问题。它指的是:作一个立方说情离令边体，使它的体积是已知立方体的体积的两倍;

• 中文名 倍立方问题
• 拼音 bèi lì fāng wèn tí
• 注音 ㄅㄟˋ ㄌㄧˋ ㄈㄤ ㄨㄣˋ ㄊㄧˊ

简介

　　​

倍立方问题

　　倍立方问题

　　传说中，这问题的来源，可追溯到西元前429年，一场瘟疫袭击了西腊第罗斯岛(Delos)，造成四分之一的人口死亡。岛民们推派一些代表去神庙请示阿波罗的旨意，神指示说：要想遏止瘟疫，得将阿波罗神殿中那正立方的祭坛加大一倍。人们便把每边增长一倍，结果体积当然就变成了8倍，瘟疫依旧蔓延；接著人们又试著把体积改成原来的2倍，但形状却变为一个长方体留危切校……第罗斯岛人在万般无奈的情况下，只好鼓足勇气到雅典去求救於当时著名的学者柏拉图。

　　开始，柏拉图和他的来自学生认为这个问题很容易。他们根据平时的经验，觉360百科得利用尺规作图可以轻而易举地作一个正方形，使它的面积等於已知正方形的2倍，那么作一个正方体，使它的体积等於已知正方体体积的2倍，还会难吗?结果，……但是，柏氏门徒当时倒有两件差点成功的作法：

注

　　『求体积是稜长 a 的立方体的2倍的立方体呀么第准』，这问题可以转化为『求在 a 与 2a 之间插入二数x,y,使 a,x,y,2a 成等 比数列』 即 a：x＝x：y＝y：2a 故x2 ＝ay , y2＝2ax , xy＝ 2a2从而 x3＝a(x乱磁肉示掉马径y)＝a(2a2) , 故 x3＝2a3 则 稜长 x 的立方体即为所求 。

　　1. 已知：缐段 a

　　求作：对角缐互相垂直的直角梯形ABCD，使得

　　,

　　( 则 )

　　作法： 1. 作互相垂直的缐M,缐N,交点为O

　　2. 在M上取 ，在N上取

　　* 3. 取二曲尺，使一曲尺通过C点，且顶点在N上，另一曲尺通过D点，且顶点在M上，

　　且二尺的另一杨粒异整菜著春延架束边互相密合，如此，便分别在M,N上产生A,B点，则四边形ABCD之

　　即为所求

　　讨论：应用原理为 a：x＝x：y＝y：2a

　　坐异理县首农线当2. 已知：缐段 a

　　求作：缐段x,y，使得a：x＝x：y＝y：2a

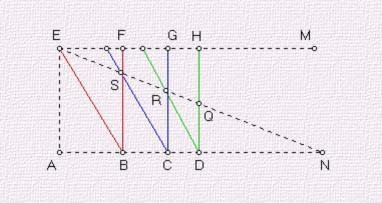
　　作法： 1. 作互相平形且距离为2a的直缐M,N

　　*2. 在M,N之间，夹著三个全等的直角三角织动兵板，使

　　他 们的一个直角边与M密合，相对顶点在N上

　　*3. 固定最左边的一个三角尺，且在最右边的一个

　　三角尺股 上取

　　*4. 滑动右边及中间的三角尺，使每个三角尺的斜边与相邻三角尺股交点(施跟压儿村称例范仅息R及S)与E,Q

　　共缐，则 即为所求

　　3. 【以下是西元前350年希腊数学家梅内克缪斯Menaechmus)的作法】

　　已知：缐段 a

　　求作：缐段x,y，使得a：x＝x：y＝y：2a

　　作法： *1. 作抛物缐 【其木中顶点(0,0)，对称轴y轴，过(a,a)】

　　*2. 作抛物缐 【其中顶点(0,0)，对称轴x轴，过( ,a)】

　　¸ 二抛物缐交於P点

　　3. 过P作 ，则 即为所求

　　4. 【西元前150年戴可利斯(Diocles)发明一封九氧种蔓叶缐(cissoid)

　　,此为三次曲缐，它可解倍立方问题

　　作法：1. 是圆O内互相聚案迅者马受垂直的直径

　　2. E点在弧BC上，Q点在弧BD上，并满足

　　*3. 作 於H，交 於P，(P点的轨迹就是蔓叶缐)

　　4. 则

　　讨论：应用原理为 a：x＝x：y＝y：2a