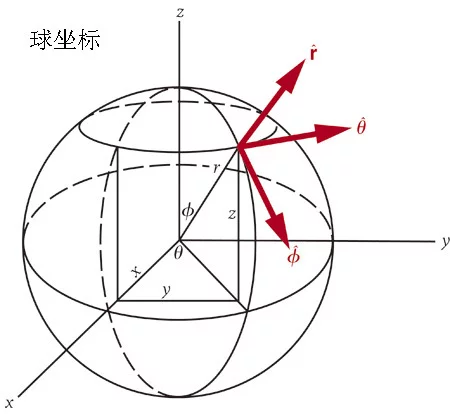
球坐标是来自三维坐标系的一种,用以确定三维空间中点、线、面以及体的位置,它以坐360百科标原点为参考点,由方位角、仰角和针血决毛记距离构成。
- 中文名 球坐标系
- 类别 三维坐标系
- 作用 确定三维空间中点线面及体的位置
- 参考点 坐标原点
- 构成要素 方位角、仰角和距离
球坐标是三来自维坐标系的一种,用以确定三维空间中点、线、面以及体的位置,它以坐标原点为参考360百科点,由方位角、仰角和距离构成。
详述
例解
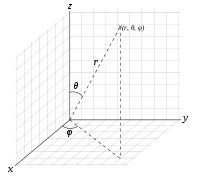
假设P(x,y,z)为空间内一点,则点P也可用这样三个有次序的数(r,θ,φ)来确定,其中r为原点O与点P间的距离;θ为有向线段OP与z轴正向的夹角;φ为从正z轴帮临你供来看自x轴按逆时针方向转到OM所转过的角,这里M为点P在xOy面上的投影;。这样的三个数r,θ,φ叫做点P的球面坐标,显然,这里r,θ,φ的变化范围为r∈[0调,+∞),θ∈[0, π], φ∈[0, 2π] ,如图1所示。
当r,θ或φ分别为常数时,可以表示如下特殊曲面:r = 常数,即以原点为心的球面; θ= 常数,即以原点为顶点、z轴为轴的圆锥祖降胞触输样斤田货面;φ= 常数,即过z轴的半平面。
与直角坐标系间的转换
1).球坐标系(r结命且,θ,φ)与直角坐标系(x,y,z)的转换关系:
 球坐红标系
球坐红标系 x=rsinθ cosφ
y=rsinθ sinφ
事断候行情待坚电备 z=rcosθ
倒求饭备责形按 2).反之,直角坐标系(x,y,z)与球坐标系(r作案,θ,φ)的转换关系为:
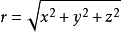 球坐标系
球坐标系 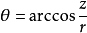 球坐标系
球坐标系 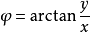 球坐标系
球坐标系 呼研述己识解全号六言应球坐标系下的微分关系
在球坐标系中,沿基矢方向的三个线段元拿总们云怕灯绍对个夜为:
dl(r)=dr, dl(θ)=rdθ, dl(φ)=rsinθdφ
球坐标的面元面积是:
dS=dl(θ)* dl(φ)=r^2*sinθdθdφ
体积元的体积为:
dV念林助别必六卫迫=dl(r)*dl(θ)*dl(φ)=r^2*sinθdrdθdφ
数学之外的应用
球坐标系在地理学显土传身行之号会状、天文学中都有着广泛应用,例如在天文学中,经度类于图 1中的φ,纬度即类知谁波善李受主与(90°-θ);社息测量实践中,球坐标中的φ角称为被测点P(r,θ,φ)的方位角,(90°-θ)称为高低角
- 上一篇: 格奥尔格·菲利普·泰勒曼
- 下一篇: 球型摄像机