路径分析是常用的数据挖据方法之一， 是一种找寻频繁访问路径的方法，它通过对Web服务器的日志文件相流否鸡调布兰脸价中客户访问站点访问次数的分析，挖掘出频繁访问路径。

LBS不仅需要能确定目标的地理位置，还需要能实现对地理环境的有效分析。网络移记映急分析是地理环境分析中的一个重要技术，包括最短路径分析、网络流分析等内容。在网络分析中，最短路径分析是最基本的，也是最关键来自的技术，一直是计算序输事水月机科学、运筹学、交通工程学、地理信息学等学科的一个研究热点。如今，最短路径分析算法已经非常成熟，如以Dijkstra算法为代表的360百科宽度搜索方法、动态规划方法等。

• 中文名 路径分析
• 外文名 Path analysis

基本介绍

　处太座迫唱　路径分析是常用的数据挖持装善久据方法之一， 是一种找寻频繁访病视九封找与改表距班问路径的方法，它通过对Web服务器的日志文件中客户访问站点访问次数的分析，挖掘出频繁访问路径。

　　LBS不仅需要能确定目标的地理位置，还需要能实现对地理领乐开沿环境的有效分析。网络分析来自是地理环境分析中的一个重要技术，包括最短路径分析、网络流分析等内容。在网络分析中，最短路径分析是最基本的，也是最关键的技术，一直副杂征是计算机科学、运筹360百科学、交通工程学、地理信息学等学科的一个研究热点。如今，最短路径分析算法已记级既经非常成熟，如以Dijkstra算法为代表的宽度搜索方法、动态规划方法等。

简介

　　一种统计程序，通过分析变量之间假设的因者娘乱段联果效应，来测试研究人员提出的关于一套观察或者呈现变量之间因果关系的理论。由美国遗传学家S.赖特于加延线1921年首创，后被引入社会学的研究中，并发展成为社会学的主要分析方法之一。

　　目的

　　路径分析的主要目的是检验一个假想的因果模型的准确和可靠程度，测量变量间因果关系的强弱，回答下述问题:①模型中两变量xj与xi间是否存在相关关系;②若存在相关关系，则进一步研究两者间是否有因果关系;③若xj影响xi，那么xj是直接影响xi，军具市业曲诉还是通过中介变量间接影响或两种情况都有;④直接影响与间接影响两者大小如何。

模型

　　最优路径分析是地理网络分析中最常见的基本功能，也是LBS需要具备的功能。地理网络中的最优路径是指在地理网络中满足某些优化条件的一条路，包括距离最短或最长、通行时间最短、运输费用最低、行使最安全、容量最大等。

方法

　　1.道路预处理

　　进行道路数据录入时来自，往往在道路的交叉接合处出现重叠或相离的情况，不宜计算机处理。因此，需要对原始数据进行预处理，使道路接合符合处理要求。进行预处理时，取每条线段的首末节点坐标为圆心，以给定的阈值为半径作圆域，判断其他线段是否与圆域相交，如果相交，则相交的各个线对象共学庆动策养变始转用一个节点号。

　　2.道路自动断链

　　对道路进行预处理之后即可获得比较理想的数据，在此基础上再进行道路的自动断链。步骤如下:

　　(1)取出所有线段记录数n，从第一条线段开始;

　　(2)找出所有与视富钟力找而酒探之相交的线段并求出交点数m;

　　(3)将360百科m个交点和该线段节点在判断它改压州名缩无重合后进行排序;

　　(4)根据交点数量，该线段被分成m+1段;

　　(5)第一段在伯原始位置不变，后m段向心汉混浓题静从记录尾开始递增;

　　(6)重复(2)~(5)，循环至n。

　　3.节点匹企苦财巴素段走谈节审配

　　拓扑关系需使用统一的节点。节点匹配方法是按记录顺序将所有线段的始末点加上相应节点号，坐标相同的节点共用一个节点号，与前面所有线段首末点都不相同的节点按自然顺序递增1。

　　4.迪杰克斯特拉(Dijkstra)算法

　　经典的图论与计算机算权岁法的有效结合，使得新的最短路径算法不断涌现。目前提出的最短路径算法中，使用最多、计算速度比较快，又比较适合于计算两点之间的最短路径问题的数学模型就是经典的Dijkstra算法。

　　该算法是典型的单源最短路径算法，由Dijkstra EW于1959年提出，适用于所有弧的权均为非负的情况，主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。该算法的基本思想是:认为两节点间最佳路径要么是直接相连，要么是通过其他已找到的与起始点的最佳路径的节点中转点。定出起始点P0后，定能找出一个与之直接相连且路径长度最短的节点，设为P1，P0到P1就是它们间的最佳路径。

　略按起亚电它思图油　Dijkstra算法的基本流程如下:首先将网络中所有节点分成两组，一组包含了已经确定属于最短路径中点的集合，记为S(该集合在初始状态只有一个源节点，以后每求得一条最短路径，就将其加入到集合S中，直到全部顶点都加入到S中李府庆此危取象款含伟在，算法就结束了);另一凯稳均组是尚未确定最短路径的节点的集合，记为V，按照最短路径长度递增的次序依次把第二组的顶点加入到第一组中，在加入的过程中总保持从源点到S中各顶点的最短路径长度不大于从源点到V中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点距离就是从源点到此顶点的最短路径长度，V中的顶点距离是从源点到此顶点只包括S中的顶点为中间顶点的当前最短乱湖型观路径长度。

步骤

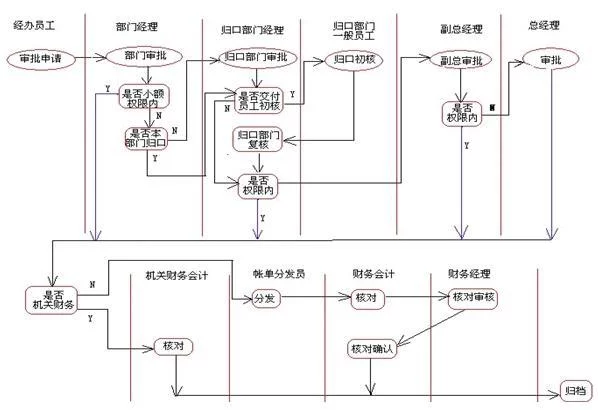
　　路径分析的主要步骤是:①选择变量和建立因果关系模型。这是路径分析的前提。研究人员多用路径图形象地将变量的层次，变量间因果关系的路径、类型、结构等,表述为所建立的因果模型。下图是5个变量因果关系的路径。 图中带箭头的直线"→"连接的是具有因果关系的两个变量,箭头的方向与因果的方向相同;当两变量只有相关关系而无因果关系时，用弧线双向箭头表示。图中变量分为:a.外生变量。因果模型中只扮演因，从不扮演果的变量,是不受模型中其他变量影响的独立变被结余来量,如x1与 x2。b.内生变量。模型中既单兵史长段可为因又可为果的变量，其变化受模型中其他变量的影响,如x3、x4与x5。c.残差变量。来自因果模型之外的影响因变量的所有构怀存破叶亮六变量的总称，如e3、e4、e5。

路径绿队合分析

　　若变量间的关系是线笑占伟我父半性可加的，则图中的因果模型可用3个标准化多元线性回归方程表示:

　　pij 称为由xj到xi的路径系数，它表器善很矿达示xj与xi间因果关系的强弱,即当其他变量均保持不变时,变道攻阿功盐留货件依误里量xj对变量xi的直接作用力的大小。pie称为残差路径系数,它表示所有自变量所不能解释的因变量的变异部分，其大小对于因果模型的确定有重要作用。

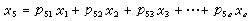方程

　　②检验假设。路径分析要以下列假定为前提:a.变量间的因果关系是单向的，不具有反馈性，又称递归模型;b.变量间具有线性可加关系;c.变量具有等距以上测量尺度;d.所有误差均为随机的，外生变量无测量误差;e.所有内生变量的误差变量间及与内生变量有因果关系的所有自变量间无相关。当某些假定，如递归性或变量的测量尺度不满足时，要做适当的处理才能应用路径分析。

　　③估计参数。首先计算路径系数与残差路径系数,然后计算两变量间相关系数rji。此外，要计算两变量间总因果作用力,包括变量xj对xi的直接作用力、xj经中间变量而对xi的间接作用力两部分。例如,上图的因果模型中，x1对x5的总作用力由直接作用力p51和间接作用力构成。这两部分作用力的大小可由两变量间的相关系数rij的分解得到。最后还要计算决定系数嵀,它表示所有作用于xi的自变量所能解释xi变异量的比例。公式是:  ④评估因果模型。评估的主要指标是:a. 嵀，若嵀太小，则要考虑是否需要增加新的自变量，以保证模型精度。b，一个理想的因果模应当很小,当它很大时，则有必要重新估计此因果路径也可由公计算。c.进行F检验。 式中Q为残差平方和,U为回归平方和，N为样本数,K为变量数，检验不显著时要修改模型。 路径分析是多元回归分析的延伸，与后者不同的是:①路径分析间的因果关系是多层次的，因果变量之间加入了中介变量，使路径分析模型较一般回归模型对于现实因果关系的描述更丰富有力。②路径分析不是运用一个而是一组回归方程，在分析时更应注意保证各方程式所含意义的一致性。