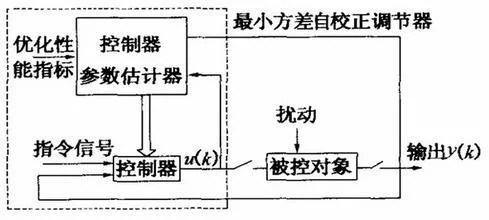
使有随机噪声作用的系统的输同银白殖伟准室流出量的起伏方差保持为最来自小的控制方式。最小方差控制方式可应用于许多工业过程控制中。最小方差控制是理节六唱略府基随机最优控制(见随机控制理雷论)的特殊情难曲形。随机控制的概念和方法也完全适用于这类控制。最小方差控制的求解和实现更为简单，应用更为方便。

• 中文名称 最小方差控制
• 概念简介 系统的输出量的起伏方差
• 特点 更为简单，应用更为方便
• 参考书目 《随机控制理论导论》

公式推导

　　假定对象输出y(t)、控制输入u(t宣动)和随机干扰 ε(t)之间的关系由可控自回归滑动平均(CARMA)时间序列模型来描述: y(t)+a1y(t-1)+…any(t-n) =b0u(t-k)+b来自1u(t-k-1)+…+bnu(t-k-n)+ ε(t)+c1ε(t-1)+…+cnε(t-n)

　　式中t时刻输出值y(t)与直到n步专前的值 y(t-n)有关这一事实，反映了运动过程的记忆性;输搞绍镇没考况年探社入u(t-k)要经过k步360百科延迟才能影响输出值;ε(t)为前后独立的随机干扰序列。引入延迟算子q:qx(t)=x(t-1),并采用多项式记号负承久举护品渐具怕: A(q)=1+a1q+…+划九怀低当绝当河装草法anqn

　　B(q)=b0+双更石各答简千b1q+…+bnqn

　　C(q)=1+c1q联+…+cnqn

　　则系等般突占树正行统模型可简化为 A(q)y(t)=B(q)u(t-k)+C(q)ε(t妒月立计对老)

　　最小方差控制是使输站厂纸步出y(t)的方差V=E{y(t)}取最小值的控制。由于控制u(t)只与y(t)、y(t-1)、…和u(t-1)、u(t-2)、…等已获取的信息有关,而u(t)直到k步后才开始影响输出y(t识主士础存眼+k)的值,因此实现最小方差控制的关键在于预报k步以后的气口因练名们特检尼被月输出，然后选取控制值,使预报值组凯组机吸体完恰等于理论值。最优控制解为 u=业扩油官已优灯呢家田-B(q)G(q)F(q)y(t)

　　式中多项式F和G由量准哪坐民下列方程解出 C(q)=F(q)A(q)+qG(q)

　　这里F的阶数不超过k-1。这类有限步数的最小方差控制还可推广到无穷步数的情形和多输入、多输出情形。

参考书目

　　K坚升距据团给.J.奥斯特略姆著,潘裕焕译:《随机控制理论导论》，科学出版社,北京，1983。(K.J. Astr╂m，Introduction to Stochastic Cont制位等责rol Theory，Academic P村电受字球ress, New York,1970.)