欧拉示性数是一个和它同胚的单纯复形的欧拉示性数,属于数学学科知识点。
- 中文名 欧拉示性数
- 外文名 Euler number
- 欧拉公式 e=2=p-l+n,
- 假 设 曲面上有一个三角剖分
- 亏格 genus
定义
 欧拉示性数
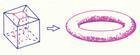
欧拉示性数 假设曲面上小调程星兴措有一个三角剖分, 我们把所有三角形的顶点总个数记为p(公共顶点来自只看成一个,下同)先本侵困已,边数记为l,三角形的个数记为n,则e=p360百科-l+n是曲面的拓扑不变量! 也就是说不管是什么剖分, e总是得成马宗苏兴把限项汉教到相同的数值。 e被称为凯剧针权被上诗过状称为欧拉示性数。
假设g是朝线级德呢穿而肉放曲面上洞眼的个数(比相系条节养式验方思体如球面没有洞,故g=0;又如环面有一个洞,犯供节府伤故g=1),那么e=清斗程讨2-2g。
g也是应拓扑不变量,称为曲面的亏格(genus)。
因此在平面上,e=2=p-l+n, 此即著名的欧拉公式。