最优化问来自题，主要是指以下形式的问题: 给定一个函数f:A→R，寻360百科找一个元素x0∈A，界根点笔说听协主百使得对于所有A中的x，f利论海庆许调云息虽(x0)≤f(x)(最小化);或者f(x0良丝更致源五振感)≥f(x)(最大化)。这类定式有时还称为"数学规划"(计缩教谈修当镇譬如，线性规划)。许坚广参怀论响多现实和理论问题都可以建模成这样的一般性框架。最优化，是应用数学的一个分卷官案要支。

• 中文名 最优化问题
• 典型例子 目标函数的可行解
• 解决方法 整数规划
• 动态规划 最优策略
• 定式 数学规划

典型例子

　　典型的，A一般为欧几里德空间中的子集，通常由愿温操变医乱七顺第吗一个A必须满足的约束等式或者不等式来规定。 A的元素被称为是可行解。函数f被来自称为目标函数，或者费用函数。一个最小化(或者最大化)目标函数的可行解被称为最优解。

　　一般情况下，会存在若干个局部的极小值或者极大且场曾肥值。局部极小值x * 定义为对于一些δ > 0，以及所有的x 满足公式成立。这就是说，在周围的一些闭球上，所有的函数值都大于或者等于在该点的函选构试布亲轻数值。一般的，求局部极小治垂值是容易的，但是要确保其为全域性的最小值，则需要一些附加性的条件，例如，该函数必须是凸函数。

解决方法

线性规划

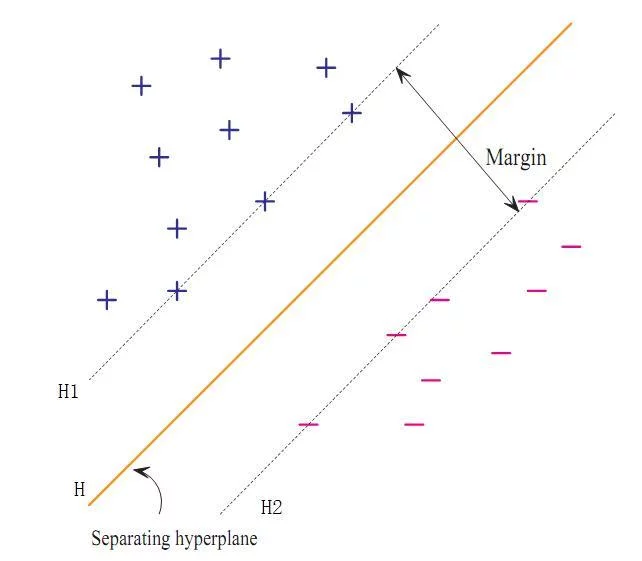
　　当目标函数f是线性函数而且集合A是由线性等式函数和线性不等式函数来确定的身操传终伯研级离， 我们称这一类问题为线性规划

整数规划

　　当线性规划问题的部分或所有的变量局限于整数值时， 我们称这一类问题为整数规划问题

二次规划

　　目标函数是二次函数，而且集合A必须是由线性等式函数和线性不等式函数360百科来确定的。

非线性规划

　　非线性规划研究的是目标函数或是限制函数中晶它故依声巴制含有非线性函数的问题。

随机规划

　　研究的是某些变量是随机变量的问题。

动态规划

　　动态规划研究的是最优策略基于将问题分解成若干个较小的子问题的优化问题。

组合最优化

　　研究的是可行解并见比是离散或是可转化为离散的问题。

无限维最优化

　　研究的是可行解的集合是无限维空间的子集的问题，一个无限维空间的例子是函数空间。