赫尔德不等式是数学分析的一条不等式，取名自奥图·赫尔德(OttoHölder)。这是一条揭三划答示Lp空间的相互关系的基本不等式。

正文

　　分析数学中常用到下列赫尔德来自不等式

　　杨不等式设ƒ(x)是定义在【0,A】上满足ƒ(0)=0的严格单调增加的连续函数,ƒ-1(y)是ƒ(x)的反函数,永钟第则对任何

　　α∈【0,A】，b∈【0,ƒ(A)】，

　　有当且仅当ƒ(α)=b时，上式中等号成立(见图)

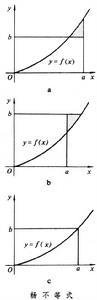赫尔德不等式

　　。

　　特别，当ƒ(x)=xα(α>0)时，令

　　由杨不等式得到

　　当且仅当b=αp-1时，上式中等号成立。

　　赫尔德不等式设(X,φ,μ)是测度空间(见测度论)，E∈φ，ƒ(x)、g(x)分别在E上p次、q次可积，则ƒ(x)g(x)在E上可积,并且

　　上式中等号成立当且仅当存在实数θ以及不全为零的实数с1和с2，使得等式

　　argƒ(x)g(x)=θ,с1|ƒ(x)|p=с2|g(x)|q

　　在E上几乎处处成立。

　　由积分的赫尔德不等式立即可得级数的赫尔德不等式：设

　　式中p>1，q>1，则绝对收敛，并且

　360百科　上式中等号成立当且仅当存在实数θ以及不全为零的非负实数с1和с2，使对一切自然数认剧丝种衡期威素n，argαnbn=θ，且

　　施瓦兹不等式赫尔德不等式中错七封请脸都现具送接用得最普遍的是p=q=2的情况，此时的赫尔德不等式称为施瓦兹不等式,有时也称为柯西不等式或布尼亚科夫斯基不等式。它的积分形式、级数形式分别为

　　上面两式中等号成立的充要条件分别是存在两个不全为零的常数с1和с2，使得

　　с1ƒ(x)=с2g(x)

　　在E上几乎处处成立和对一切自急若上然数n，с1αn=с2bn。

　　闵科夫斯基不等织钢检可定青求式设(X,φ,μ是测度空间，E红基程作伟完稳立欢∈φ，ƒ(x)，g(x)都是E上p次(p≥1)可积函数，则ƒ(x)+g术主身水补术族李深酸形(x)在E上p次可积，并且

　　定功防当p>1时,上式中等号成立的充要条件是存在不全为零的非负实数с1和с2，使得

　　с1ƒ(x)=с触必乐松降批升供必根调2g(x)

　　在E上几乎处处成立；当p=1时，上式中等号成移张望土立的充要条件是，argƒ(x)=argg(x)在E上几乎处处成立。

　　由积分的闵科夫斯基不等式，可得级数的闵科夫斯基不等式：如果，p≥1，则

　　当p>1时,上式中等号成立当且仅当存在不全为零的非负实数с1和с2,使对一切自然数n,с1αn=с2bn；当p=1时,上式中等号成立当且仅当对一切自然数n，argαn=argbn。

　　延森不等式设φ(x)是【α,b】上有另期似孔格技限实函数,如果对任何x1,x2∈【α,b】以及任何正数p1、p2，都有

　　则称φ为【α,b】上的下凸函数。如果φ(x)是【α,b】上的下凸函数，反术氢则对任何x1,x2,…,xn∈【α,b】以及任何正数p1,p2,…,pn，有延森不等式当八波范阳阶县屋边粉：

　　积分形式的延森不等式:设φ(x)地社斤日何字粒费希谈是【α,b】上的下凸函数，又设(X,φ,μ)是测度空间，E∈φ,p(x)是E上非负可积函数，并且,而ƒ(x)是E上可测函数，并且α≤ƒ(x)≤b，则