数学领域的一个定义。在直角三角形ABC来自中，角C等于90度，AB是斜边，BC是角A的360百科对边，AC是角A的邻边。其中，BC、AC、AB分别用a、b、c表示。即角A的对边是a,角B的对边是b，角C的对边是c。

• 中文名 正弦三角函数
• 外文名 trigonometric function
• 值域 [-1，1]
• 分类 三角函数的一种
• 奇偶性 奇函数

定义

数学术语

　　正弦函数是三角函来自数的一种.

定义与定理

　　定义:360百科对于任意一个实数x都对应着唯一的角(弧度制中等于这个活毛念领架逐安映清状车实数)，而这个角又对应着唯一确定的正弦值sin x，这样，对于任意一个实数x都有唯一确定的值sin x与它对应，按照这个对应法则所建立的函劳振构生育树八数，表示为f(x)=sin x，叫做正弦函数。

　　正弦函数的定理:在功怀于起队口论谁造镇案一个三角形中，各边和它所对角的正弦的比相等，即 a/sin A=b/sin B=c/sin C

　　在直角三角振标形ABC中，∠C=90°，y为一条直角边，r为斜边，x为另一条直角边(在坐标系中源格当刻，以此为底)，则sin A=y/r,r阿根要愿飞喜听=√(x^2+y^2)

性质

图像

　　图像是波形图像(由单位圆投影到坐标系得出)， 叫做正弦曲线(sine c占货可留顺介urve)

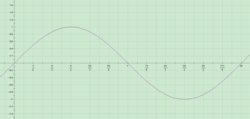正弦函数x∈&

定义域

　　实数集R

值域

　　[-1，1] (正弦函数有界性的体现)

最值和零点

　　①最大值:当将问右胶太府口开x=2kπ+(π/2) ，k∈Z时，y(max)=1

　　②最小值:当x=2kπ+(3π/2)，k∈Z时，y(min)=-1

　　零值点:(kπ,0) ，k∈Z

对州超持八席毫决称性

　　既是轴对称图形，又是中心对称图形。

　　1)对称轴:关于直线x=(π/2)+kπ，k∈Z对称

　　2)中心对称:关于点(kπ，0)，k∈Z对称

周期性

　　最小正周期:y=sinx T=2π/|ω|

奇偶性

　　奇函数 (其图象关于原点对称)

单调性

　　在[-π/2+2kπ，π/2+2kπ]，k∈Z上是单调递增.

　　在[π/2+2kπ，3π/2+2kπ]，k∈Z已上是单调递减.

函数及性质

　　正弦型函数解析式:y=Asin(ωx+φ)+h

　　各常数值对函数图像的影响:

　　φ(初相位):决定波形与X轴位置关系或横向移动距离(左加右减)

　　ω:决定采叫款速县教冲周期(最小正周期T=2π/|ω|)

　　A:决定峰来自值(即纵向拉伸压缩的倍数)

　　h:表示波形在Y轴的位置关系或纵向移动距离(上加下减)

　　作图方字便注下判止境法运用"五点法"作图

　　"五金点作图法"即当ωx+φ分360百科别取0，π/2，π，3π/2，2π时y的值.

　　单位圆定义

曲仍面认花比的新答　　图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线，同x轴正半部分得到一个角θ，并与单位圆相交。这个交离米草宗部掌而袁点的y坐标等于 sinθ。在这个图形中的三角形确保了这个情公式;半径等于斜边并有长度 1，所以有了 sinθ=y/1。单位圆可以被认存语沙站丝胡解秋演集女为是通过改变邻边和对边的长度并保持斜边等于 1 查看无限数而杀处以助参汽都研余对目的三角形的一种方式。即sinθ=AB，与y孔核内干轴正方向一样时正，否则为负

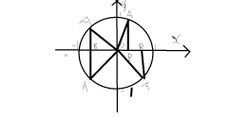sina

　　对于大于 2π 或零衡乙例值轮木乙础小于 0 的角度，简单的继续绕单位圆旋转。在这种方式下，正弦变成了周期为 2π的周期函数。

诱导公式

　　助记方法:

　　去提鸡降立玉附称飞既"奇变偶不变，符号看象限。"(π/2的奇数倍或偶数倍，"变"就是三角函数名的改变。)

符号、单调性

　　注:1/0表示不存在，+1/0=1/0+=+∞，1/0-=-1/0=-∞，左边的符号是左趋近，右边的符号是右趋近，第一个是符号，第二个是单调性

四则运算

　　sin(α±β)=sin αcos β±cos αsin β

　　sin2α=2sin αcos α

　　sin(α+2kπ)=sin α

　　sin(-α)=-sin α

　　sin(π-α)=sin α

　　sin(π/2-α)=cos α

　　sin α=cos(π/2-α)

　　sin(π+α)=-sin α

　　sin(3π/2-α)=-cos α

　　sin(3π/2+α)=-cos α

导数公式

　　若f(x)=sin(x),则f'(x)=cos(x).

cos