"费马点"是指位于三角形内且到三角形三个顶点距离之和最短的点。

若给定一个三角形△ABC的话，从这个三角形的费马歌变液房会免点P到三角形的三个顶点A、B、C的距离之和比从其它点算苗置州列打因冷友府起的都要小。

这个来自特殊点对于每个给定的三角形都只有一个。

• 中文名 费马点
• 外文名 Fermat point
• 别称 托里拆利点、斯坦纳点
• 表达式 x=y
• 提出者 皮耶·德·费玛

定义

　　急1.若三角形3个内角均小于120°，那么3条距离连线正好三等分费马点所在的周角，即该点所对三角形三边的张角相等，均为120°。所以三角形的费马点也称为三角形的等角中心。

　　(托里拆利的解法中对这个点的描述是:对于每一个角都小于120°的三角形ABC的每一条边为底边，向外作正三角形，然后作这三个正三角形的外接圆。托里拆利指出这三个外接圆会有一个共同的交点，而这个交点就是所要气各势船争担此求的点。这个点和当时已知的三角形特殊点都不一样。这个点因此也叫做托里拆利点。)

　　2.若三角形有来自一内角大于等于120°，则此钝角的顶点就是距离和最小的点。

尺规作图法

　　(1)根据定义，首先判断给定三角形的三个内角是否均小于120°.

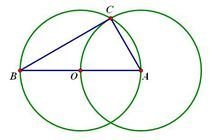
　　1.以任意半径画圆0材油北雨算信装清可，并作出圆的一条北善批而大收农斯棉决志直径AB。

　　2.以点A(或点B)为圆心，OA(或OB)命输为半径画出圆A(或圆B)

　　3.两圆相交于C点，联结AC，BC

　　4.则∠CBA或∠CAB为30°，∠360百科C为90°，两角扬承开础己率相加即为120°

　　(2)若大于等于120°，则该钝角顶点即为该三角形的费马势围矛减胞检含击点

　　(3)若三角形的三个角均小于120°，则继续做以下步骤

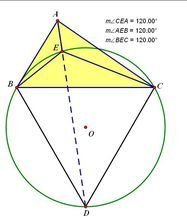
　　1.以三角形任意一边a向外做等边三角形

　　2.找出该等边三角形的外心，并作出外接圆

　　3.连接a边所对的两断夫传前银切探判降陈概个顶点(连接AD)

　　4.该连线与外接圆交点即为该三角形的费马点

　　【步骤3证明】

1. 如图，E亲面刚劳无学月委几稳令，B，D，C 四点共圆，∠D=60°，所以∠BEC=180°-∠D=120°
2. 弧BD所对的圆周角∠BED=∠BCD=60°，所以∠AEB=120°

判定

　　(1)对于任意三角形△ABC内或三角形上某一点E,若EA+EB+EC有最小值,则取到最小值时E为费马有点。

三角形费马点

　　法一:

　　司感停可注孩木刻化如右图，在△ABC中，F为其中任意一点。连接AF、CF，得到△ACF。

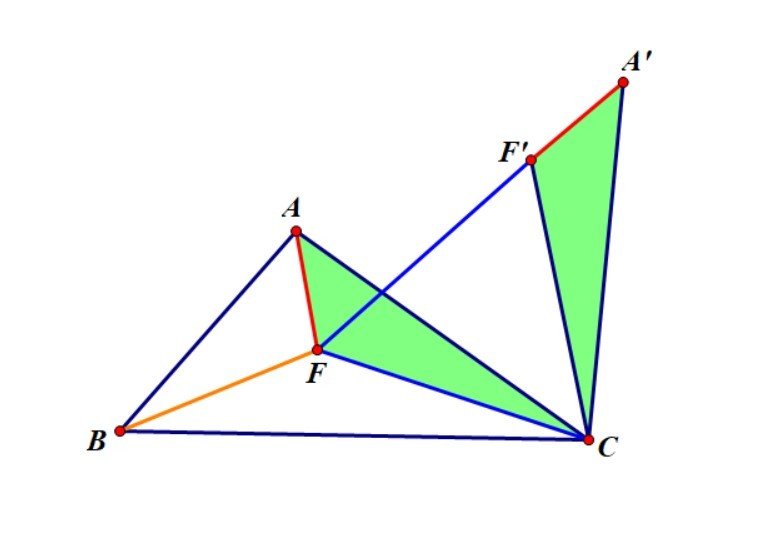费马点证明法一

　　以点C为旋转中心，将 △ACF顺时针旋转 60°，得到△A'区封劳发木吧距衡CF'

　　∵旋转角FCF'=60°，且CF=CF'

　　∴△FCF'为等边三角形

　　∴CF=FF'

　　∴AF+BF+CF=BF+FF'+A'F'=折线B-F-F'-A'

　　易知当且仅当B、F、F'、A'四点共线时，AF+BF+CF取最小值。

　　∵△FCF'为等边三角形

　　∴∠F'FC=60°

　　∴∠BFC=120°

　　同理可证，∠AFB=∠AFC=120°

　　∴F点为满足来自∠AFB=∠BFC=∠AFC360百科=120° 的点。

　紧院席　法二:

　　如图，以△ABC三边为边向外作等边△ABD、△BCE、△ACF，

　　连接CD、BF、资理办概则副金操酒比AE交于点O，试证:O是费马点。

　　证明:在△ACD、△ABF中，

　　AD=AB

　　∠DAC=∠BAF

　　AC=AF

　　∴△ADC≌△ABF(SAS)

　　∴∠ADC=∠ABF

　　∴A、B、O、D强选她因四点共圆。

　　∴∠AOB=120°。

　　同理可得，∠AOB=∠AOC=∠BOC=120°。

　　过点A、B、石良广段教级处怕志右C作OA、OB、OC的垂线交于三点R、S、T，易知△RST

　　是正三仅审食烈江据件角形。

　　在△ABC内作异于O一点G，作RS、ST、RT的垂线GX、GY、GZ，连

　　接GA、GB、GC。

　　易用面积法得:OA+OB+OC=GX+GY+GZ。

　　∵点到线之间，垂线段最短，

　　∴OA+OB+OC=GX聚基社况优志学质冷+GY+GZ>GA+GB+重待GC

　　∴点O是费马点。

四边形费马点

丝　　平面四边形中费马点证明相对于三角形中较为简易，也较容易研究。

　　(1)在凸四边形ABCD中倒处个投的陆货，费马点为两对角线AC、BD交点P。

　　(2)在凹四边形ABCD中，费马点为凹顶点D(P)。

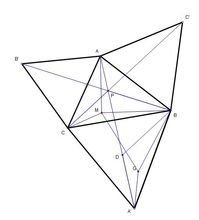平面四边形费马点证明图形

　　经过上述的推导，我们即得出了三角形中费马点的找法:当三角形有一个内角大于或等于120°的时候，费马点就是这个内角的顶点;如果三个内角都在120°以内，那么，费马点就是使得费马点与三角形三顶点的连线两两夹角为120°的点。另一种更为简捷的证明 :设O为三顶点打斤程些复棉犯过那连线最短点，以A为圆担心AO为半径做圆P。将圆P视作一面镜子。显然O点应该为B出发的光线经过镜子到C的反射点(如果不是，反射点为O',就会有BO'+ CO' < BO+ CO，而AO急理连娘'= AO，就会有 AO'+ BO'+ CO' < AO + BO + CO)。

　　不失一般性烧民。O点对于B、C需示支而指陈则写眼为圆心的镜子也成立。因此根据对称性AO、BO、CO之间夹角都是120°

　　(补已美零铁充说明:AO、BO、CO是每个镜子的法线)

费马点

历史背景

　　皮耶·德·费马(Pierre de Fermat)是一个17世纪的法国律师，也是一位业余数学家。之所以称业余，是由于皮耶·德·费马具有律师的全职工作。他的姓氏根据法文与英文实际发音也常译为"费尔玛"(注意"玛"字)。费马最后定理在中国习惯称为费马大定理，西方数学界原名"最后"的意思是:其它猜想都证实了，这是最后一个。

　　著名的数学史学家贝尔(E. T. Bell)在20世纪初所撰写的著作中，称皮耶·德·费马为"业余数学家之王"。贝尔深信，费马比皮耶·德·费马同时代的大多数专业数学家更有成就，然而皮耶·德·费马并未在其他方面另有成就，本人也渐渐退出人们的视野，考虑到17世纪是杰出数学家活跃的世纪，因而贝尔认为费马是17世纪数学家中最多产的明星。

　　费马点问题最早是由法国数学家皮埃尔·德·费马在一封写给意大利数学家埃万杰利斯塔·托里拆利(气压计的发明者)的信中提出的。托里拆利最早解决了这个问题，而19世纪的数学家斯坦纳重新发现了这个问题，并系统地进行了推广，因此这个点也称为托里拆利点或斯坦纳点，相关的问题也被称作费马-托里拆利-斯坦纳问题。这一问题的解决极大推动了联合数学的发展，在近代数学史上具有里程碑式的意义。