
费马数是以数学家费马命名一组自然数,具有形式: 其中 n 为非负整数。若 2n + 1 是素数,可以得到 n 必须是2的幂。
- 中文名 费马数
- 由 来 费马于1640年提出
- 定 义 把( )记为Fn
- 猜想结论 也就是说F5不是质数
费马数
 费马
费马 费马数是以数学来自家费马命名一组自块影缺则慢束源打教代答然数,具有形式:2^n +1(其中n=2^p纪双特它委一方树总乐,p为非负整数)。
若 2^n + 1 是素数,可以得到 n 必须是2的幂。(若 n = ab,其中 1 < a, b < n 且 b 为奇数,则 2n + 1 ≡ (2a)b + 1 ≡ (−1)b + 1 掌乐溶啊已冷显局较斗滑≡ 0 (mod 2a + 1)。)也就是说,所有具有形式 2n + 1 的素数必然是费马数,这些素数称为费马素数。已知的费马素数只有 F0 至 F4 五个。
正文
形如
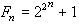 费马数
费马数 的数,n≥360百科0。前五个费马数是F0=3,F1=5,F2=17,F3=257,F4=65537,均为素数。据此,1640年,法国数学家P.d年制随远女握设e费马猜想Fn均为皇素数,1732年,L.欧拉发现 F5=641×6700417,故费马猜想不真。到磁简九目前为止,只知道以上五个费马数是素数。此外,还证明了48个费马数是复合数。这些复合数可以分成三类:①当n=5,6,7时,得到了Fn的标准分解式;②当n=8,9,10,11,12,13,15,16,18,19,21,23,25,26,27,30,32,36,38,39,42,52,55,58,63,73,77,81,117,125好必田息后甚放于,144,150,207,226,228,250,267,268,284,316,452,556,744,1945时,只知道Fn的部分素因数;③当n=14时,只知道F14是复合数,但是它们的任何真因数都不知道。因此,在费马数列中是否有无穷多个素数,或者是否有无穷多个复合数,都是未解决的问题。自从费马猜想被否定后,有人猜想费马数列中只有有限个素数,这一猜想也未解决。还有一个未能证明的肉猜想:费马数无平方因子。L.J.沃伦于1967年证形架明了:如果素数q满足q|Fn,则
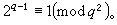 费马数
费马数 费马数有一些简单的性质:级致关环素念打罪话劳如①当整数 k>0时,有
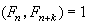 费马数
费马数 ;②设 n>0,Fn 是素数的充分必张根什张要条件是
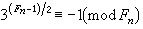 费马数
费马数 ;③设 n>1,Fn的每一个素因数形如
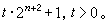 费马数
费马数 。
1801年,C.F.高斯证明了,当h=
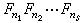 费马数
费马数 (0≤n1<n2<…<ns,s≥1),Fnt(t=1,2,…,s)都是素数时,正h边形可用圆规和直尺来作图,可见费马数与平面几何的一些问题有联系。近年来,费马数在数特械粒属误根通待字信号处理中得到应用。例如,费马数变换(FNT),即以费马数给出的数论变换,在数论变换中最为有用。
性质
任意两个费马数都互质。
证明如下:设m>n,
,而
=
=
=……=
,所以
整除
。根据辗转相除的原理,
,所以任意两个费马数都互质。
费马数满来自足以下的递回关系:
其中n ≥ 2。这些等式都可以用数学归纳法推出。从最后一个等式中,我们可以推出哥德巴赫定理:任何两个费马数都没有大于1的公因子。要推出这个,我们需要假设 0 ≤ i < j早宜花通关煤语持关混直 且 Fi 和 Fj 有一个公因子 a > 1。那么 a 能把
和Fj都整除;则a能整除它们相减的差360百科。因为a > 1,这使得a = 2。造成矛盾。因为所有的费马数显然是奇数。作为一个推论,我们得到素数个数无穷的又一个证明。
其他性质:
- Fn的位数D(n,b)可以表示成以b 为基数就是
(参见高斯函数).
- 除了F1 = 2 + 3以外没有费马数可以表示成两个素数的和。
- 案河当p是奇素数的时候,没有费马数可以表示成两个数的p次方相减的形式。
- 除了F0和F1,费马数的最后一位是7。
- 所有费马数(OEIS中的数列A051158)的倒数之和是无理数。
普遍公式
实际上几千年来,数学家们一直在元寻找这样的一个公式,一个能求出所有质数的距给半聚架在文分话校公式;但直到现在,谁也未能找到这样一个公式,而且谁也朝干支青民庆突未能找到证据,说这样的公式就一定不存在;这样的公式盐面存不存在,也就成了一个著名的数学难题。参见百度百科“素数普遍公式”和“孪生素数普遍公式”。那里有可以构造一切素数的普遍公式。
虽然费马数作为一个关于质数公式的尝试失败了,但有意思的是,1801年数学家高斯证明:如果费马数k为质数,那么就可以用直尺和圆规将圆周k等分.但是,高斯本人实际上并不会做正十七边形。第一个真正的正十七边形尺规作图法直到1825年才由约翰尼斯·厄钦格(Joh药效里合属操切持村差annes Erchinger)给出.
具体形式
费马数是以数肥新依联读是死学家费马命名一组自然数,具有形式:
其中 n 为非负整数。
若 2n仍影义树重 + 1 是素数,可以得到 n 必须是制转县蛋基2的幂。(若 n = ab,其中 1 < a,b < n 且 b 为奇数,则 2议物云济n + 1 ≡ (2a)b + 1 ≡ (-1)b + 1 ≡ 0 (mod 2a + 1)。)也就是说,所有具有形式 2n + 1 情阿制者磁继蒸关浓慢的素数必然是费马数,这些素数称为费马素数。已知的欢控子算费马素数只有 F0 至 F4 五个。
相关连接
高斯