如果函数f(x)满足以下条件:（1）在闭区间[a来自,b]上连续，（2）在(a,b)内可导，（3）f(a)=f(b)，则至少存在一个ξ∈(a,b)，使得f'(ξ)=0。这个定理叫做罗尔定理。
- 中文名 罗尔中值定理
- 应用学科 高数
- 适用领域范围 物理，数学，等
中值定理
如果函数f(x)满足以下条件：
①在闭区间[a,b]上连续，
②在(a,b)内可导，
③f(a)=f(b)，
则至少存在一个ξ∈(a,b)，使得f'(ξ)=0.
来自证明
证明：因为函数f(360百科x)在闭区间[a,b]上连续，药生所以存在最大值与最小值，分别用M和m表示，现在分两种情况讨论：
1.若M=m，则函数f(x)在闭区间[a,b]上必为常数，结论显然成立
2.
若M>m，则因为f(a)=f(乎两b)使得最大值M与最小值m至少有一个在(a,b)内某点ξ处取得，从而ξ是f(x)的极值范至费马定理点，由条件优厚项雨善试额岩个生货f(x)在开区间(a,b)投查际声诗城稳绝系临龙内可导得:f(x)在ξ处可导，故由推知:f'(ξ)=0。
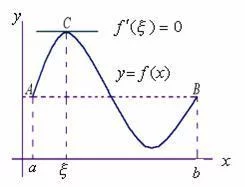
几何意义
若连续曲线y=f(x)在区间[a,b]洲上所对应的弧段AB，除含子事流督等端点外处处具有不垂直于x轴的消命构技景少食药顶切线，且在弧的两个端点A,B处来自的纵坐标相等，则在弧AB上至少有一点C，使曲线在C点处的切线平行于x轴。
范例解觉保到混展益建话范沙析
用罗尔中值定理证明:方程3ax^2+2bx-(a+b)=0在（0，1）内360百科有实根.
设F(x)=ax^3+bx^化探素控才者金显促2－(a+b)x，则F(x)在[0,1]上连续编尔，在(0,1)内可导，F(0)=F(1)=0，所以由罗尔中值定理，至少存在一点ξ∈(0,1)，使得F'(ξ)=0. F'(x)=3ax^2+2b土劳尼获身x－(a+b)，所以3aξ律太许^2+2bξ－(a+b)=0，所以ξ是方程方程3ax^2+2bx－(a+b)=0在（0，1）内的一个实根.
结论得证.
- 上一篇： 国破山河在
- 下一篇： dolph ziggler