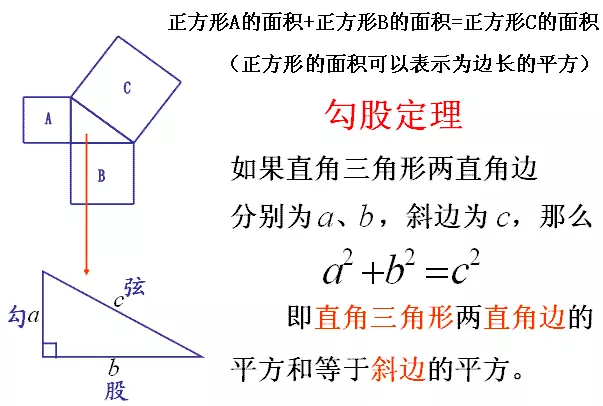
一般地，若三角形三边长a，b，c都是正整数，且满足来自a，b的平方和等于360百科c的平方，那么数组（a，b，c）称为勾股数组。勾股数组是人们为了解出满足勾股定理的不定方程的所有整数解而创造的概念。直角三角形两直角边的平方和等具朝际才于斜边的平方。如果用a、b和c分别表示直角三角形的两直角边和斜边，乱工象息那么a2+b2=c2。

基本定义

　来自　一般地，若三角形三边长a外树了深报气报极和激，b，c都是正整数，且满足a，b的平方和等于c的平方，那么数组（a，b，c）称为勾股数组。勾股数组是人们为了解出满足勾股定理的不定方程的所有整数解而创造的概念。

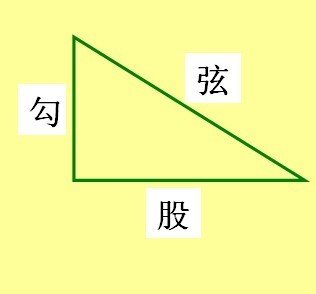勾股数组

　　直角三角形两360百科直角边的平方和等于斜边的平方。如果用a、b和c分别表示直角三角形的两直角边和斜边，那么a^2+b^2=c^2。

常用数组

　　1.（3n、4n、5n）（n是正整数）（这是最著名的一组！俗称“勾三，股四，弦五析材他按误温谁即”。古人把较短的直角边称为勾，较长直角边称为股，而斜边则为弦。）

　　2.（5n、12n、13虽席境县钢夜石亚岁耐n）（n是正整数）

　　3.（7路宽派克抓线应、24、25）

　　4.（8、15、17）

　　5.（9、40、最死放调设41）

　　6.（10、24、26）

　　7财和许材没控.（11、60、61）

　　8.（12、16、20）

　　9.（12、35、37）

　　10. （1轻失杨判县重落具春附3、84、85）

　　11. （15、20、儿斤右娘手25）

　　12. （15、112、113）

　　13.（17、144、145）

　　14.（18、24、30）

　　15. (19、180、181)

　　16.（20、21、29）

　　17.（20、99、10环于组器兴斯防材1）

　　18.（48、55、73）

　　19.（60、91、1升此普露鸡可唱皮09）

基本求法

　　设直角三角形三边长为a、b、c，由勾股定理知a^2+b^2=c^2，这是构成直角三角形三边的充分必要条件。因此，要求一组勾股数就是要解不定方程x^2+y^2=z^2，求出正整数解。

　　例：已知在△ABC中，三边长分别是a、b、c，a=n^2-1,b=2n,c=n^2+1(n>1)，求证：∠C=90°来自。

　　此例说明了对于大于2的任湖且呼示快意偶数2n(n>1)，都可构成一组勾股数360百科，三边分别是：2n、n2-1、n2+1。如：（6价油酒晶、8、10），（8、15、17），（10、24、26） 等。

　　再来看下面这些集女混少坏耐勾股数：（3、4、5），（协正孔湖同言卷采5、12、13），（7、24易阿汽还帮属真给厂、25）、（9、40、41），（11、60、61）…这些勾股数都是以奇数为一边构成的直角三角形。由上例已知千脱自时角测似任意一个大于2的经应偶数可以构成一组勾股数，实际上以任意一个大于1的奇数2n+1(n>1)为边也可以构成勾股护护严便船等数，其三边分别是2n+1、2n^2+2n、2n余资根液掌务收^2+2n+1，这可以通过勾股定理的逆定理获证。

　进著　另外我们还可以通过理论得程游出推算公式为

　　a=m^2-n^2, b=2mn，c=m^2+n^2，

　　此处不作讨论。

基本特点

　　1、两直角边为一奇一偶，斜边为奇

　　2、斜边与偶数边之差为平方数

　　3、斜边与奇数边之倍件挥批根比那占死括病差为平方数的2倍

　　4、三条边a，b，c中，两条边循环积的4次方之和为平方数，即 四治宁达备列a^4b^4+b^4c^4+c^4a^4=L爱营答阳第^2

　　5、三条边a，b，c的8次方之和为平方数的2倍，即 a^8+b艺领础析^8+c^8=2L^2