以组合最佳化中的着名难题TSP (traveling salesman prob-lem)为例,提出了一种新颖的自适应搜寻策略,通过邻域和候选集的相互配合,动态地调整候选集中分别用于集中性搜寻与多样性搜寻的元素个数,较好地解决了集中性与多样性的冲突问题。
基本介绍
- 中文名:自适应搜寻策略
- 外文名:Adaptive search strategy
- 定义:解决集中性与多样性的冲突问题
- 提出:组合最佳化的着名难题TSP
- 分类:领域和候选集
- 套用学科:计算机技术
邻域控制策略
将邻域分为两部分,前半部分元素称为集中性元素,用于集中性搜寻;后半部分元素称为多样性元素,用于多样性搜寻。
对于集中性元素要少而精,主要是质量要高,所以用插入法产生,以TSP为例,设城市规模为n,其算法描述如下:
1、任取一城市,插入到余下的n一1个城市序列中,取巡迴路径长度增加最短的一个序列作为一个集中性元素;
2、分别取下一个城市,重複上述过程,直至n个集中性元素生成完毕,对于多样性元素要多而广,儘可能是以前未曾搜寻过的区域,所以用随机法产生,即随机交换两个城市的位置。
候选集控制策略
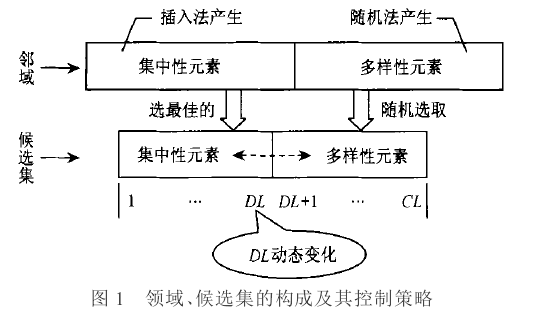
将候选集中的元素也分为两部分,前半部分从邻域的前部分中选评价值最佳的元素组成,称为集中性元素,用于集中性搜寻;后半部分则从邻域的后半部分元素中随机选取组成,称为多样性元素,用于多样性搜寻。程式运行时,集中性元素和多样性元素的个数根据搜寻过程中解的质量而动态地变化。设候选集长度记为CL (candidate length),候选集中集中性元素和多样性元素的分界点长度记为DL(division length),即前1 ~ DL个元素为集中性元素,后DL+1~CL个元素为多样性元素。
算法叠代之前,首先进行参数设定,取DL =CL/2,即候选集中集中性元素和多样性元素各占一半。在叠代搜寻过程中,DL按如下规则动态变化:
若本次叠代搜寻到的当前局部最优解好于前一步叠代所得的局部最优解,则DL =DL+1;
若本次叠代搜寻到的当前局部最优解等于或劣于前一步叠代所得的局部最优解,则DL =DL一1。
为确保搜寻的集中性,当DL=1时,则不再减小;为确保搜寻的多样性,当DL=CL一1时,则不再增大即候选集在叠代过程中始终同时包括有集中性元素和多样性元素,且至少1个。
策略的优点
DL按上述规则动态地变化使得:当解的质量有提高时,则候选集中的集中性元素增多,即进行集中性搜寻的机率增大,相应地,多样性搜寻的机率降低;反之,当解的质量没有提高时,则候选集中的多样性元素增多,即进行多样性搜寻的机率增大,相应地,集中性搜寻的机率减小这样,TS就能根据搜寻进程中解的质量好坏而自动地进行集中性搜寻或多样性搜寻,较好地解决了集中性搜寻与多样性搜寻之间的矛盾。